Предисловие 2020 года:
Я задумал эту книгу очень давно. Затем бросил на полпути, и уже набранный текст чуть было не пропал, кочуя с диска на диск, с компьютера на компьютер. И я понял – мне будет жалко, если книга просто бесследно исчезнет, так и не родившись. То, что Вы здесь прочтёте, большей частью было написано лет пятнадцать назад. Я постарался закончить начатое, дополнить и увязать обрывочные главы, пока еще голова моя что-то помнит из физики и прежних моих рассуждений, обсуждений, споров в интернете, доводов и выводов. Может, кому-то будет любопытно и даже полезно это прочесть. Поэтому я начинаю публиковать на своей странице в сети первые, уже написанные главы книги, попутно корректируя их. И, если потребуется, понемногу буду дописывать новые.
Предисловие
Я не знаю, дорогой читатель, волнуют ли тебя тайны мироздания. Ощущаешь ли ты замирание сердца и душевный трепет в те редкие мгновения, когда перед тобой приоткрывается завеса тайны, научной загадки? Когда сами собой складываются нужным образом в мозгу незримые кирпичики и догадка вдруг освещает новым светом то, что ты никак не мог понять раньше, или, наоборот, считал обыденным и простым, а там, оказывается, под покровом кажущейся простоты, таились удивительные чудеса? Надеюсь, что – да. И если так, то, я уверен, ты знаешь, каким захватывающим бывает это чувство. Это ощущение прозрения, знакомое, наверно, подавляющему большинству людей. Вот только не у всех оно связано с физикой.
Чувство это бывает столь ярким и восхитительным, что само служит достаточной наградой за часы, дни, а иногда и годы, потраченные на учебу и поиски истины. И что примечательно: открытие, уже сделанное кем-то, по-прежнему способно быть волнующим озарением для тебя лично. Не беда, что слава первооткрывателя досталась другому человеку – ты все равно ощутишь радость от того, что дотянулся до мысли знаменитого предшественника, стал его сознательным последователем, поднялся на ту же ступеньку, где и он стоял когда-то. Да и сам путь к этой ступеньке может быть оригинальным, необычным и увлекательным – только твоим. Для читателей, принадлежащих к славному племени студентов, добавлю, что так оно и будет, если, читая учебники и слушая лекции, вы будете думать своей головой, а не только передирать в спешке чужие конспекты перед экзаменом.
Тайны и чудеса можно искать в разных областях науки, и не в ней одной, конечно. Кого-то манят психология, философия, традиции и опыт древних учений востока; кто-то ищет разгадку тайн бытия и вовсе вдали от наук – в искусстве, в мистике, в религии, в астрологии. Не говоря уже о том, что почти все мы с удовольствием балуем себя доступным суррогатом из выдуманных загадок: фантастикой, детективами, играми и прочим. Дело в том, что значительных научных загадок не так уж много. Точнее, загадок и тайн в науке предостаточно, но только немногие из них способны поразить воображение и заметно повлиять на наше мировоззрение.
Не желая никоим образом обидеть все прочие науки, осмелюсь высказать своё частное мнение, что в области физики количество таких фундаментальных тайн особенно велико. Ибо именно физике приходится иметь дело с первоосновами природы, с самыми базисными понятиями – материей, пространством, временем…
Я учил физику во второй половине 20 века – века, коронованного как «век физики». А в физике 20 века давно и прочно царил Альберт Эйнштейн, гениальный ученый, автор одной из самых важных и фундаментальных теорий за всю историю науки, изменившей в корне традиционные представления о мироздании. Наслушавшись отовсюду, в том числе, от своих более эрудированных школьных друзей, обрывочных, но интригующих сведений и выводов из теории относительности, я с нетерпением ждал, когда же мне эту теорию методично и обстоятельно разжуют преподаватели.
Увы! Разочарования начались еще в школе. Хоть я и учился в «продвинутой» физико-математической школе, но теория относительности (специальная) в школьном курсе скорее упоминалась, чем изучалась. В учебнике говорилось о том, что классическая физика на рубеже 19-го и 20-го столетий зашла в тупик из-за невозможности обнаружить среду, в которой распространяется свет и прочие электромагнитные колебания. А также описывался опыт Майкельсона, который устанавливал загадочную, с волновой точки зрения, независимость скорости света от его направления – вдоль или поперек движения Земли в космическом пространстве. Далее формулировались два основных постулата СТО (Специальной Теории Относительности) Эйнштейна:
• Равноправие всех инерциальных систем отсчета, в плане выполнения всех физических законов;
• Постоянство скорости света во всех инерциальных системах.
Уж не помню, было ли там приведено лоренцево преобразование координат, заменяющее прежнее линейное (а учебников тех давно уж нет под рукой); возможно, что и было. Все равно, этого было совершенно недостаточно, чтобы осознать глубину идей и перемен, связанных с именем великого физика. Не помню, чтобы кто-нибудь из нас сильно расстраивался по этому поводу. Мы полагали, что уж в институте нам все станет ясно. И я стал ждать поступления в институт.
Мне повезло: я поступил в очень солидный ленинградский ВУЗ – ЛПИ (Ленинградский Политехнический институт), на недавно созданный факультет Технической Кибернетики, где попал на кафедру Автоматизированных Систем Управления. Там нам читали отменный курс математики и достаточно объемный курс физики: три семестра общая физика и еще два – теоретическая, в общей сложности, два с половиной года. Причем, в программе курса теоретической физики черным по белому значился раздел – «Специальная теория относительности».
Открывая этот раздел, наш молодой преподаватель – очень серьёзный и вдумчивый, но немногословный, и, в силу небольшого еще преподавательского опыта, довольно скованный молодой человек, – сказал примерно следующее:
– Я не хотел бы вдаваться в словесные трактовки и философские рассуждения о теории относительности, поскольку вас они могут только запутать. Тот, кто хочет глубже ознакомиться с историей и существом вопроса, может самостоятельно почитать литературу, которая имеется в избытке. Моя же задача – научить вас решать конкретные задачи и системы уравнений. И в таком «прикладном» свете вся специальная теория Эйнштейна сводится к сравнительно простым преобразованиям координат, известным как преобразования Лоренца.
И тут он в считаные секунды набросал на доске широко известные формулы, описывающие пересчет координат и времени, при переходе из одной системы координат в другую, движущуюся со скоростью “v” относительно первой.
– Из этих соотношений легко видеть, что скорости, превышающие скорость света, для физических систем невозможны, – добавил наш лектор, – так как для них выражение под корнем обращается в отрицательную величину.
Утверждение, надо признать, абсолютно справедливое и исчерпывающее, с математической точки зрения. Ограничившись оным, он быстро перешел к каким-то более сложным уравнениям, то ли механики, то ли электродинамики, которых я, по прошествии многих лет, совершенно уже не помню, и которые требовалось отредактировать с учетом релятивистского преобразования координат.
Нет, я понимаю – есть люди с незаурядными способностями к физике и математике, у которых так счастливо устроена голова, что им достаточно увидеть уравнения, и они сразу ухватывают и физический смысл формул, и их связь с другими законами, и уже ничего больше им не нужно объяснять. Но я сам, к несчастью, не такой, и подозреваю, что большинство людей тоже. Нам нужно все долго обдумывать, примерять и пробовать, пока мы не почувствуем, что что-то поняли. Так что, дорогие гении и большие ученые, эта книга может показаться многим из вас пустой и затянутой болтовней. Тогда советую без сожалений забросить ее в мусорную корзину, и заняться более полезным делом – клянусь, я не обижусь.
Итак, моя надежда освоить теорию относительности в рамках учебного процесса была похоронена. Поняв, что помощи ждать неоткуда, я взялся за книги, благо даже в отцовской домашней библиотеке была пара популярных книжек на эту тему. Но и книги не оправдали моих надежд, вернее, не одолели «крепостных стен» моей косности. Я, правда, почерпнул из книг две-три важных мысли и, в каком-то смысле, лёд в моей голове тронулся, но само обоснование центральной идеи теории относительности я осилить не смог. Оно страдало, в моих глазах, недостатком ясности и досадными пропусками важных деталей в цепи логических рассуждений. Главное, оно было очень кратким. Создавалось ощущение, что авторы стремятся как можно скорее проскочить скучное и излишне сложное объяснение сути теории, и перейти к более веселым следствиям, выводам и парадоксам.
Читать же первоисточники я не рискнул, опасливо полагая, что великие физики адресуют свои работы таким же великим физикам, и не опускаются до утомительного разжевывания своих теорий для таких серых типов, как я.
Не раз потом, в разных ситуациях и по разным поводам, я возвращался мыслями к теории Эйнштейна. И только по прошествии несколько лет, после многократных плутаний в лабиринте логических противоречий, доводов и контрдоводов, я, наконец, почувствовал, что ухватил путеводную нить, за которую смогу держаться, чтобы выйти из лабиринта к свету.
Глава 1. Несколько предварительных цитат
Многие мыслители в разные эпохи указывали на связь пространства и материи. Поразительно глубокую мысль о сущности пространства можно найти у величайшего французского математика и философа 17 века Рене Декарта, который отмечал:
«…пространство совпадает с протяженностью, а протяженность связана с телами; таким образом, нет пространства без тел и, следовательно, нет пустого пространства».
Остановитесь и вдумайтесь: НЕТ пустого пространства без тел! Абсолютно ключевая мысль для понимания всего дальнейшего. Пустота становится реальным физическим объектом только тогда, когда в ней есть НЕЧТО, помимо пустоты.
Сам Эйнштейн, отвечая на заданный ему вопрос о сути теории относительности, сказал: «Суть такова: раньше считали, что если каким-нибудь чудом все материальные вещи исчезли бы вдруг, то пространство и время остались бы. Согласно же теории относительности вместе с вещами исчезли бы пространство и время». В своей статье “Относительность и проблема пространства”, Эйнштейн рассказывает об исторической подготовке и реализации новой концепции бытия. Он объясняет, что в механике Ньютона пространство и время, с одной стороны, и материальные частицы, с другой – существуют раздельно. «При этом существенным обстоятельством, – пишет Эйнштейн, – является то, что «физическая реальность», независимо от познающих ее субъектов, представлялась состоящей, по крайней мере, в принципе, из пространства и времени, с одной стороны, и из постоянно существующих материальных точек, движущихся по отношению к пространству и времени, с другой. Идея независимого существования пространства и времени может быть выражена следующим образом: если бы материя исчезла, то остались бы только пространство и время (своего рода сцена, на которой разыгрываются физические явления)»¹. Переход от такого представления о пространстве и времени, как о сцене, на которой разыгрываются физические явления, к новому представлению, состоит в утверждении:
когда физические процессы не разыгрываются, сцены нет, она не существует.
В предисловии к очередному изданию Эйнштейн писал:
«В этом издании я добавил Приложение V, в котором изложил свои взгляды на проблему пространства вообще и на изменения наших представлений о пространстве, возникающие под влиянием релятивистской точки зрения. Мне хотелось показать, что пространству и времени нельзя с необходимостью приписать раздельное существование независимо от действительных объектов физической реальности. Физические объекты находятся не в пространстве, но эти объекты являются пространственно-протяженными. На этом пути концепция “пустого пространства” теряет свой смысл»¹.
Приведу еще несколько цитат, справедливость которых, надеюсь, станет очевидной по ходу изучения СТО:
«Время возникло вместе с миром. Оно, стало быть, принадлежит этому миру, поэтому «в то время», когда не существовало Вселенной, не было никакого времени» (В.Гейзенберг).
«Главный враг знания не невежество, а иллюзия знания» (С. Хокинг).
«Единственное, что мешает мне учиться, – это полученное мной образование.» (А.Эйнштейн).
«Математика это самый совершенный метод водить самого себя за нос» (А.Эйнштейн).
Именно эта последняя мысль убедила меня написать книгу без всяких формул.
=================================================
1) Эти цитаты из книги:
Борис Кузнецов. «Эйнштейн. Жизнь. Смерть. Бессмертие.»
Глава 2. Мысленный эксперимент “Один в космосе”

Представьте себя космонавтом, вышедшим в открытый космос из своего звездолета, летящего куда-нибудь к Марсу. Вы видите вокруг далекие звезды и галактики и чувствуете себя крохотной песчинкой, затерянной в бескрайнем космосе. Страшновато, не правда ли… Теперь вообразите нечто намного более страшное: представьте, что внезапно все звезды и галактики исчезли, исчезла вообще вся материя из окружающего Вас космоса, включая Ваш корабль, Солнце и планеты. Остались только Вы в невесомости и кромешной тьме.
Скажите, что теперь Вы думаете о размерах космоса? Простирается ли, по-прежнему, необъятное пространство за пределами того расстояния, на которое Вы можете протянуть руку или ногу? Конечно, Вы можете его вообразить. Но будет ли иметь такое воображаемое пространство какую-то связь с реальностью? Ведь Вы лишены всякой возможности перемещаться в нем. Вы можете, конечно, дрыгать конечностями и вертеть головой, но никакого влияния на положение Вашего тела в абсолютно пустом пространстве это не окажет. Само понятие «положение» потеряло всякий смысл.
А почему бы не представить, что весь космос сжался до размеров некоего «пузыря пространства», ограниченного зоной досягаемости Ваших рук и ног? Пространство за пределами этого пузыря является лишь математической абстракцией, не способной оказывать на реальность ни малейшего воздействия. Значит, с точки зрения физика, оно не является элементом реального мира, или, попросту, – не существует.
Заметим, что и о собственных размерах у Вас не может быть определенного мнения. Вы вполне можете предположить, что Вас волшебным образом «раздуло», как сказочную Алису, до размеров прежней Вселенной, или наоборот, сжало почти в точку.
Ну и, наконец, – время. Даже если шутник, изъявший всю материю из окружающего космоса, украл и хронометр с Вашей руки, Вы, скорее всего, решите поначалу, что с ходом времени ничего не произошло. Но, поразмыслив, усомнитесь и в этом. Вы поймёте, что единственным эталоном хода времени для вас остались процессы, происходящие в вашем собственном теле: биение пульса, движение мышц… Сама быстрота течения Ваших мыслей связана, как известно, со скоростью протекания различных физико-химических процессов в мозгу. Если предположить, как мы только что делали, что с Вашими размерами произошла некая метаморфоза, то вполне вероятно, что и скорость всех этих процессов изменилась, только Вы этого, разумеется, не заметили, потому что изменились сами. А со стороны за Вами наблюдать некому.
А если бы, вместо Вас, в космосе оказалась неживая кукла из нестареющего, не подверженного самораспаду материала, вряд ли можно было вообще говорить о течении времени. Кукла так и повисла бы вечно в пространстве непонятного размера.
Проведенный нами мысленный опыт не служит иллюстрацией или объяснением теории относительности. Однако в нём мы оперируем теми базисными понятиями физики, к которым обращается и теория Эйнштейна, и которые подвергаются в ней, как мы увидим дальше, существенному переосмыслению. Внимательно вглядываясь и заново обдумывая знакомые, простые, «интуитивно понятные» физические термины – пространство, размер, время, – мы начинаем лучше понимать их неоднозначность, неабсолютность. И, если при этом шатаются и рушатся некие старые догмы, коренящиеся в наших головах и мешающие движению вперед – тем лучше.
Главное, что я хотел продемонстрировать, – это то, что и в рамках старой классической модели понятия пространства и времени, так же как понятия размеров и скоростей, бывают только относительными, и неразрывно связаны с существующими материальными объектами. Я хотел, до всякой теории, дать некое предчувствие, что эти понятия вообще не могут существовать сами по себе в реальной действительности, то есть, являются не просто связанными, но зависимыми от объектов материального мира. Абсолютно пустое пространство, в котором нет материи, утрачивает характеристики размера и времени – те единственные характеристики, которые мы ему неосознанно приписываем: бесконечно большое пустое пространство неотличимо от бесконечно малой точки, миллиарды лет в пустом пространстве неотличимы от мгновения. Говоря языком физики, или, если это вам ближе, языком программиста, пространство и время являются свойствами материальных объектов, а не самостоятельными объектами.
Вот почему-то этот последний шаг – от неразрывной связи к зависимости, вторичности по отношению к материи – дается наиболее трудно, в том числе, и некоторым философам вполне материалистических взглядов, которые пытаются осмыслить основы современной физики. Они сознают, что пространство и время неотделимы от материи, но, вместе с тем, изо всех сил стремятся сохранить их, как равноправные с материей, независимые сущности.
Господа философы, ну подумайте еще раз – какими странными и мистическими вещами были бы бесконечное пустое пространство и неизвестно как текущее время, в отсутствие вещества и событий. Разве не достаточно, что в нашем мире есть уже одна, в высшей степени загадочная, субстанция, называемая материей, что вы пытаетесь присовокупить к ней еще две? Разве не учили нас, что в науке надо стремиться к уменьшению количества базисных понятий? Именно в этом состоит один из фундаментальных методологических принципов – принцип “Бритвы Оккама”, в кратком виде гласящий: «Не следует множить сущее без необходимости».
Понимаю, что сегодня многие наслышаны также о кривизне пространства и о расширении пространства Вселенной. Это может Вас смутить: раз пространство имеет способность «искривляться и расширяться», то почему его нельзя считать самостоятельной материальной субстанцией? Тут нужно четко понимать, что кривизна пространства, о которой говорится в Общей Теории Относительности, это просто кривизна траекторий материальных тел, движущихся в поле гравитации. То, что планеты кружат вокруг Солнца, – это и есть «кривизна» околосолнечного пространства. То, что подброшенный камушек падает на землю, – это пресловутая «кривизна пространства» у поверхности Земли. Т.е., она вызывается материальными телами, и проявляется через траектории движения материальных тел.
Что касается расширения Вселенной, то здесь мы рискуем попутать следствие и причину. Истинных причин этого расширения мы пока не знаем, физики говорят о «тёмной энергии». Энергия, как и гравитационное поле, штука совершенно материальная, и приписывать наличие некой собственной энергии пустому пространству – довольно странно. В момент Большого взрыва (начальный момент существования нашей Вселенной, согласно представлениям современной физики) вся материя находилась в одной точке, и пространство тоже было замкнуто, ограничено этой крошечной точкой. Не было никакого пространства «вокруг», точно также, как не было никакого времени до момента Большого Взрыва. Т.е., пространство было там, где была материя. И потому, логичней предположить, что пространство растет вследствие разбегания материи, а не наоборот. То есть, пространство расширяется благодаря некой энергии, присущей самой материи, или поступающей извне (возможно, из другого пространства, другого измерения?).
Может быть, когда-то в будущем взгляды физиков на пустое пространство изменятся, но это будет уже иная физика, и на справедливость выводов СТО она, скорее всего, не повлияет.
Итак, дорогие читатели, если вы принимаете такой строго материалистический подход, согласно которому пространство и время – всего лишь свойства, характеристики материи, то, может быть, вас не шокирует, что некоторые неожиданные особенности поведения материи отразятся и в необычном поведении этих свойств. Или скажем это несколько иначе: если в наблюдении за поведением материи обнаружатся необъяснимые логические противоречия, а устранить их, вернее, объяснить и согласовать с опытом, можно будет корректировкой таких свойств материи, как расстояния, скорости, и ход времени, это не покажется вам невыносимо тяжелой жертвой?
А странности, уж поверьте, не заставят себя ждать.
Глава 3. Система отсчета
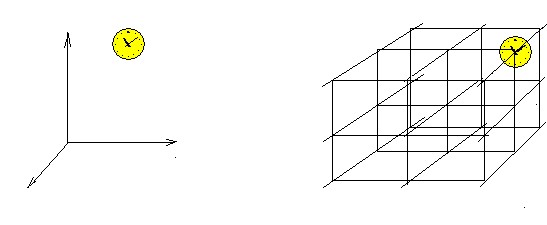
Но не будем спешить. Прежде, в этой главе давайте разберемся с таким необходимым понятием как «система отсчета» (СО). Понятие это обычно включает «систему координат», то есть три перпендикулярные воображаемые оси, уходящие в бесконечность, или пространственную координатную сетку, тоже воображаемую и бесконечную, и, в дополнение к ней, – символические часы, т.е. некий способ измерения интервалов времени.
Постойте! – воскликните Вы, – но в таком виде система отсчета являет собой «живое воплощение» как раз тех понятий, которые мы только что объявили несуществующими – пустого бесконечного пространства и независимо ни от чего текущего времени. Увы, Вы правы – именно эта знакомая со школы, привычная картинка «системы отсчета» может стать серьезным тормозом при первом знакомстве с теорией относительности. Все дело в том, что, не будучи привязанной хоть к какому-то материальному объекту, она является чистой математической абстракцией – очень удобной, простой, и полезной, – но абстракцией. Чтобы эту абстракцию стало возможно использовать в физических расчетах, необходимо проделать три очень важные вещи:
1. найти реальное физическое тело (объект привязки), относительно которого система отсчета либо неподвижна, либо строго определенным образом движется;
2. найти материальный эталон длины (это может быть то же самое тело, или любой другой физический объект), который будет использован для измерения расстояний и разметки сети координат;
3. снабдить систему совершенно реальными часами (виртуальные часы вы не отыщете даже у чистых математиков).
С такими оговорками система координат теряет всю свою абстрактную независимость, и становиться, как положено, удобным прикладным физическим инструментом, сделанным из материальных «деталей» и «винтиков».
К сказанному нужно еще добавить, что в СТО мы будем рассматривать только «инерциальные» системы отсчета – ИСО. Определение инерциальной системы отсчета можно найти в любом школьном учебнике физики: это система отсчета, в которой тела, не испытывающие воздействия внешних сил, находятся в состоянии покоя или равномерного прямолинейного движения.
Спросим себя: если мы захотим указать две различные системы отсчета, движущиеся одна относительно другой, разве обязательно привязывать их к разным материальным телам, разным эталонам длины, и разным часам? Нет, из нашего определения этого пока что не следует. Но, все же, для дальнейшего удобства, будем считать, что каждая система отсчета привязана к своему «воображаемому наблюдателю», который всегда неподвижно расположен в точке начала координат этой системы. Что же касается эталона длины и времени, то у нас нет пока никаких оснований считать, что один и тот же предмет не может быть эталоном длины как в той системе, где он неподвижен, так и в той, где он перемещается, и что одни и те же часы не могут считаться эталонными в обеих системах.
Положим, мы уже подыскали подходящий эталон длины и точные часы, покоящиеся в одной инерциальной системе отсчета. Что мешает нам использовать этот эталон и эти же часы для измерений длины и промежутков времени в других системах отсчета, движущихся относительно первой? Вроде бы, ничего?
Однако, задумайтесь на минутку, с чисто практической стороны, о сложности измерения длины любого движущегося предмета – к примеру, пролетающей мимо стрелы, проезжающего мимо троллейбуса… Каким образом можно замерить их длину, если Вы не имеете возможности остановить их и приложить к ним мерную ленту? Ведь, если Вы побежите рядом, то покинете свою прежнюю СО, и окажетесь уже в СО стрелы или троллейбуса. А как замерить их – к примеру, тот же троллейбус, – не покидая свою систему координат?
Есть две возможности:
Первая – засечь, в каких точках Вашей системы отсчета начало и конец троллейбуса находятся одновременно, а для этого нужны синхронизированные часы во всех точках Вашей СО.
Вторая – зная относительную скорость троллейбуса, замерить, за какой отрезок времени троллейбус (от крайней передней до крайней задней его точки) проезжает мимо некоторой точки Вашей СО. Для обоих способов измерения, как видите, требуются часы. Т.е., отсчет времени становится неотъемлемой частью измерения длины. Вскоре нам предстоит понять, что это обстоятельство имеет не только практическое, прикладное, но и очень существенное теоретическое значение.
С движущимися часами тоже придется быть достаточно осторожными – они могут, и без всякой теории относительности, внести изрядную путаницу в наблюдения. Об этом – в следующей главе про “Эффект Доплера”.
Глава 4. Классический эффект Доплера
В большинстве книг, посвященных специальной теории относительности, упоминается эффект Доплера. Без обсуждения эффекта Доплера, в самом деле, трудно обойтись, хотя для вывода основных положений СТО он нам не понадобится. Но с ним обязательно нужно разобраться, чтобы ответить в дальнейшем на очень популярный вопрос: «Как же будет выглядеть мир глазами человека, летящего в нем со скоростью, близкой к скорости света?».
Вообще, при изучении теории относительности, есть два неизбежных вопроса, которые и я себе не раз задавал: первый – «как выглядят все физические процессы, происходящие в одной СО, глазами наблюдателя другой СО, движущейся с большой скоростью относительно первой?»; а второй, самый любимый, – «как же, с какой скоростью, черт возьми, процессы происходят на самом деле???».
Ответы на них, как вы, наверно, уже догадываетесь, в релятивистской физике будут не просты. На второй вопрос, заранее признаюсь, вообще будет невозможно ответить однозначно, так как каждый наблюдатель с равным правом будет придерживаться своей шкалы расстояний, своего отсчета времени, и иногда даже разной временной последовательности для причинно-несвязанных событий. Причинно-связанные события, разумеется, сохранят свою последовательность, из какой бы системы отсчёта их ни наблюдали. Но об этом позже.
А сейчас я вас, возможно, удивлю: думаете, в классической физике ответ на оба вопроса прост и одинаков? То есть, для быстро движущегося наблюдателя происходящие события будут выглядеть так же, как для неподвижного, – а именно так, как они происходят на самом деле?… Ошибаетесь, друзья! Тут-то впервые и появляется перед нами эффект Доплера. Эффект этот, на первый взгляд, не слишком сложен, и заключается в следующем:
Если имеются некий источник периодически повторяющихся сигналов (звуковых, электромагнитных) и наблюдатель, принимающий эти сигналы, то движение наблюдателя относительно источника приводит к изменению частоты принимаемых сигналов: если источник и наблюдатель сближаются – частота принимаемых сигналов возрастает, если они удаляются друг от друга – частота падает.
Чем ниже скорость распространения сигнала, тем меньшая скорость наблюдателя относительно источника нужна, чтобы заметить эффект Доплера. А потому понятно, что эффект Доплера раньше всего обнаружился для звуковых сигналов. Если быстро приближающийся к вам поезд или автомобиль даст продолжительный гудок, то вначале вы услышите звук высокий и пронзительный, а затем, когда гудящий транспорт поравняется с вами и начнет удаляться, звук резко изменится, станет низким и басовитым. Это и есть звуковой эффект Доплера.
Обычно в качестве периодичного сигнала рассматривают синусоидальную волну определенной частоты. Тогда эффект можно выразить несложными формулами, связывающими частоту или угловую скорость, длину волны, и скорость наблюдателя. Однако это совершенно необязательно. (Вы любите формулы, читатель? Я, если честно, – не очень…) Если уж мы говорим о звуках, то подходящим периодическим сигналом может быть и отрывистый писк таймера, и бой курантов, и барабанная дробь, и кваканье лягушки…
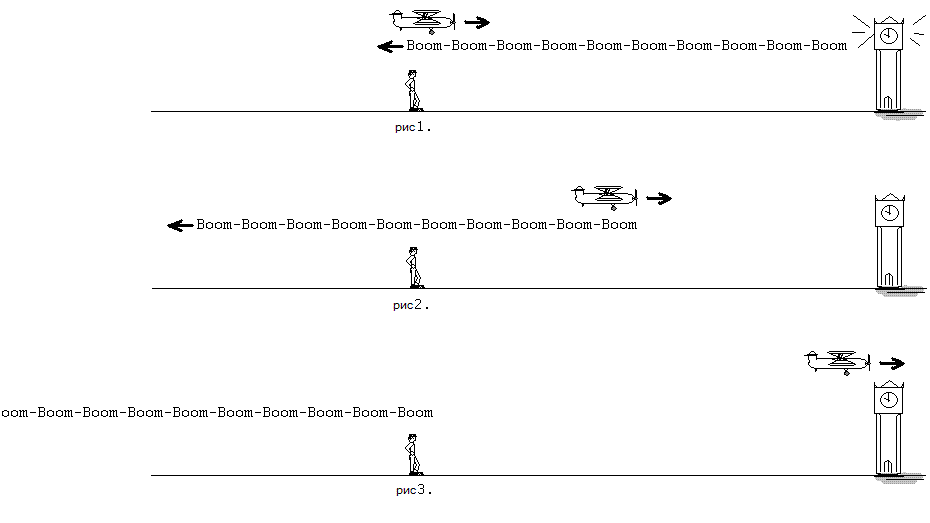
Попробуем привести наглядное объяснение эффекта Доплера без всяких формул. Будем, для примера, слушать бой часов на городской башне с некоторого расстояния (см. рисунки).
Представьте себе, что только что часы показали 10:00 утра и пробили 10 ударов, а интервал между ударами составляет ровно 1 секунду. Представьте, к тому же, что вы слушаете бой часов на таком расстоянии, что звуку от башни требуется точно 10 секунд, чтобы достичь ваших ушей. Рисунок 1 соответствует в точности тому моменту, когда колокол в часах пробил последний раз, а звук первого удара как раз долетел до стоящего наблюдателя (это вы и есть). Рисунок 2 показывает ситуацию через 5 секунд после последнего удара часов – стоящий наблюдатель успел послушать 5 ударов, и ему предстоит услышать еще пять.
Теперь добавим к нашей картине еще одного наблюдателя. Пусть им будет летчик самолета, который как раз в момент, изображенный на первом рисунке, пролетал точно над вашей головой. А летел он в направлении на башню, и со скоростью очень близкой к скорости звука. Ясно, что первый удар часов он слышал одновременно с вами. А теперь взглянем на рисунок 2, который является ключевым для объяснения. По прошествии 5 секунд летчик пролетит почти половину пути до башни. И, в то время как стоящий наблюдатель будет слышать пятый удар часов, летчик будет слышать уже последний 10-й удар. Причем, совершенно очевидно, что до этого он успел прослушать все предыдущие девять.
Что из этого следует, вы, наверно, уже догадались сами. Летящий наблюдатель услышал 10 ударов за пять секунд, т.е. часы для него били чаще и отзвонили в два раза быстрее, чем для наземных наблюдателей. Если бы на площади перед башней играл на скрипке музыкант, то летчик слышал бы любую мелодию в два раза быстрее и в другой тональности, на октаву выше.
А вот если бы самолет летел в противоположную сторону, то звук с трудом догонял бы его, и тогда все звуки летчик бы слышал, наоборот, замедленными, с растянутыми промежутками и в пониженной тональности. Как видите, мы незаметно, но совершенно логично, расширили действие эффекта Доплера с регулярно повторяющихся сигналов на все звуки вообще.
Точно такой же эффект, какой возникает для звуковых сигналов, должен возникать и для световых. Световым сигналом, в широком смысле, является любое визуальное изображение, воспринимаемое глазом или прибором, а источником такого сигнала может быть любой освещенный (либо светящийся) объект, в том числе, все те же башенные часы. Я намерен показать, что эффект, который мы наблюдали со звуковым восприятием часов, будет происходить и с визуальным. Но, чтобы заметить его, потребуется много большая скорость движения наблюдателя относительно часов, ибо световой сигнал несравнимо быстрее звука: не 300 м/с, а 300.000 км/с
Для наглядной иллюстрации светового эффекта Доплера давайте нарисуем пару картинок, очень похожую на предыдущую. Мы только изменим масштабы расстояний, для чего поместим неподвижного наблюдателя на другую планету (или на Луну), самолет с летчиком заменим на ракету с космонавтом, летящую почти со скоростью света, а башню и циферблат часов вообразим такими большими, что их можно разглядеть с Луны. Кроме того, мы добавим на часах секундную стрелку, и вместо последовательности из 10 звуковых ударов используем последовательность изображений циферблата часов, отличающихся положением секундной стрелки.
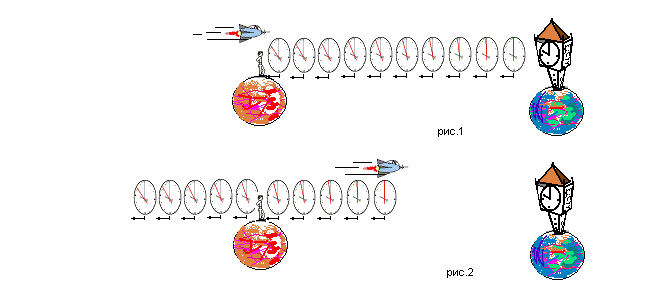
Понятно, что, если звон часов распространялся со скоростью звука, то визуальное изображение самих часов будет распространяться со световой скоростью (изображение, конечно, фокусируется уже в нашем глазу, но сути это совершенно не меняет).
Пусть, как и в прошлый раз, часы на Земле показывают 10:00 утра. Положение стрелок на циферблате, которое (на рис.1) одновременно наблюдают лунный наблюдатель и космонавт в ракете, пролетающий рядом, говорит о том, что осталось 10 секунд до 10-ти часов – секундная стрелка, показанная красным цветом, смотрит на цифру «10», и ей остается сделать десять скачков до цифры «12», прежде чем часы покажут ровно 10:00.
От момента, изображенного на рис.1, до момента, изображенного на рис.2, с точки зрения лунного наблюдателя, прошло 5 секунд. Поэтому он на втором рисунке видит секундную стрелку, показывающую на цифру 11. А вот космонавт, летящий навстречу часам со скоростью, близкой к световой, успел увидеть за это время 9 скачков секундной стрелки. С его точки зрения, уже в следующее мгновение на часах будет ровно 10:00.
И то, что происходит с циферблатом часов, относится ко всему, что космонавт видит на Земле: для него быстрее происходят все земные события, все передвижения землян кажутся ему ускоренными в два раза. И значит, время на Земле, по наблюдениям космонавта, течет в 2 раза быстрее. Это кажущееся ускорение всех визуально наблюдаемых явлений и представляет собой эффект Доплера для света в классическом понимании.
Все выглядит вполне логично, не правда ли? Тем не менее, я ясно представляю, как читатель, уже знакомый с теорией относительности, в этом месте моего повествования недоуменно пожмет плечами и даже заподозрит меня в жульничестве. И не без оснований: ведь картинки, использованные нами для объяснения эффекта Доплера, нарисованы с точки зрения наблюдателя, неподвижного относительно Земли и часов. Для движущегося же наблюдателя, как нам предстоит убедиться в скором времени, картина происходящего выглядит несколько по-иному. Если для самолета, летящего со скоростью звука, эти изменения крайне незначительны и ими можно с легкостью пренебречь, то для такой быстрой ракеты, как в нашем втором примере, изменения расстояний и времени будут настолько велики, что не заметить их будет уже невозможно. А ведь регистрирует эффект Доплера, по определению, именно движущийся относительно часов наблюдатель – тот, что сидит в ракете. И если так, то правомерна ли вообще наша попытка объяснять оптический эффект Доплера в рамках классических представлений?
Но зададимся встречным вопросом: а в каких же еще рамках нам его рассматривать, если мы пока не знакомы с теорией относительности? И как иначе должны были понимать сдвиг частоты излучения, идущего с далеких космических объектов, физики и астрономы, столкнувшиеся с этим явлением задолго до появления работ Эйнштейна? Они объясняли его примерно также, как мы в наших рисунках. И сами рисунки не содержат никакой ошибки – они точно и правдиво отражают происходящее. Только, с точки зрения классической физики, эти рисунки содержат полную, исчерпывающую информацию о наблюдаемом явлении, а с позиций релятивистской физики, рисунки абсолютно верны, но содержат не полную, а частичную правду, отражая взгляд земного и лунного наблюдателей, но не космонавта. (Известная житейская поговорка, что «неполная правда хуже вранья», в этом случае вряд ли справедлива.) Для получения полной и объективной картины, в свете теории относительности, мы должны лишь дополнить имеющиеся рисунки другой серией рисунков – сделанной летящим в ракете космонавтом. Но то, что увидит космонавт, согласно СТО, мы пока изобразить не умеем.
Я намеренно стремился избежать математических формул и точных расчетов при первом знакомстве с эффектом Доплера. Если мы выразим визуальный эффект Доплера математическими формулами, выведенными по правилам классической физики, то эти формулы окажутся впоследствии неверными для света. Но, самое главное, – они отразят беспомощность классической физики определить по величине Доплер-эффекта относительную скорость часов. Знаете, почему? Потому что кое-что очень важное ускользнуло от нашего внимания: дело в том, что для вычисления по классическим формулам требуется знать, в какой СО покоится среда, проводящая сигнал. Или, другими словами, с какой скоростью источник сигнала и наблюдатель движутся относительно среды распространения сигнала. В случае звукового сигнала, эта среда – воздух. И, если на первых двух рисунках дует сильный ветер (попутный либо встречный), то ветер непосредственно влияет на степень нарастания частоты сигнала для летчика (при встречном частота нарастает несколько медленнее, при попутном – быстрее; кому интересно, проверьте сами по классическим формулам). В случае же со световым изображением, этой средой должен был служить тот самый гипотетический «эфир», на поиски которого ушли (и до сих пор не вернулись) многие принципиальные противники СТО. А вот в СТО никакой «эфир» не понадобится. Там пустота она и есть пустота (и это огромное и бесспорное преимущество).
Вместе с тем, рисунки, отражающие суть эффекта Доплера, останутся пригодными и полезными в рамках нового релятивистского подхода. Я снова забегу вперед и скажу следующее: эффект Доплера в релятивистской физике будет учитывать разный счет времени в СО наблюдателя и источника, который нам еще предстоит понять, и потому вычисляться будет по иной формуле, чем в классической физике. Да и называться он будет «релятивистским эффектом Доплера». Но суть останется той же, и результат будет достаточно схожим:
Эффект Доплера приводит к тому, что наблюдатель, движущийся относительно всех окружающих тел и материальных объектов со скоростью, близкой к скорости света, будет видеть все что происходит впереди него смещенным в фиолетовую область спектра и, главное, происходящим в неестественно быстром темпе, как будто он смотрит ускоренное кино, а все, что остается сзади по ходу его движения, он будет видеть смещенным в инфракрасную область света, и очень статичным, почти неподвижным.
Это и есть ответ на первый принципиальный вопрос, поставленный в начале этой главы. Я привожу его здесь, еще до объяснения СТО, только потому, что практически такой же вывод следует и из классического, «до-релятивистского» эффекта Доплера, если не вдаваться в численную, формульную разницу, которая становится существенной только для околосветовых скоростей.
Сделаю еще одно, может быть, очевидное, но важное замечание: эффект Доплера существует только при условии, что скорость сигнала конечна. Если предположить, что сигнал передается мгновенно, эффект Доплера немедленно исчезнет! Так что, обнаружение светового эффекта Доплера послужило в своё время подтверждением конечности скорости света. Но об этом мы поговорим чуть позже.
В литературе по СТО приходится иногда встречать утверждение, что наличие эффекта Доплера служит одним из основных доказательств Теории Относительности. Подобное утверждение является, по меньшей мере, грубой неточностью, ибо эффект Доплера, как мы только что видели, известен и объясним в рамках классической физики. На самом деле, доказательством СТО является наблюдаемое отклонение частоты сигнала от значения, определяемого классическим эффектом Доплера (кроме этого, доказательством может служить так называемый «поперечный» эффект Доплера – уменьшение частоты в направлении, перпендикулярном движению источника сигнала). Я допускаю, что на основании этого отклонения можно получить основные формулы СТО, но такой путь построения теории относительности кажется мне запутанным и неестественным. Поэтому оставим пока в стороне этот эффект – в конце концов, он еще послужит нам, как важный факт, подтверждающий справедливость СТО и совпадающий с ее выводами. Но мы не будем использовать его, как уже было сказано в начале главы, для вывода и обоснования главных принципов теории относительности.
Глава 5. Свет – частицы или волна?
Я уже намекал на поджидающие нас странности и логические противоречия в стройной системе законов старой дорелятивистской физики, но всякий раз откладывал разговор о них на потом. Не пора ли заняться обещанными странностями вплотную? Я полагаю, что пора. Для этого нам придется задуматься о природе и свойствах света.
Свету принадлежит исключительно важная, основополагающая роль в создании СТО. Сразу оговорюсь – когда я говорю «свет», то имею в виду весь спектр электромагнитного излучения, просто так короче. Однако факт, известный сегодня каждому школьнику, – что свет является разновидностью электромагнитных волн, – вовсе не был известен ученым, жившим всего 150-200 лет назад. Более того, они даже не знали о существовании таких волн.
Но уже тогда, и даже много раньше – в VII веке, существовали, соперничая и дополняя одна другую, две модели, две концепции природы света и механизма его распространения.
Обе модели были, разумеется, механического характера, ибо механические аналогии всегда более доступны человеческому восприятию и, как правило, удобны для математического анализа. Первая из моделей, наиболее древняя, уходит своими корнями еще глубже в историю – в работы греческих (Демокрит) и арабских ученых. Согласно этой модели, свет можно представить в виде пучка быстролетящих очень маленьких твердых частичек (или «корпускул»). Самым знаменитым среди сторонников корпускулярной модели в VII веке был Исаак Ньютон.
Согласно второй модели, свет можно представить как разбегающееся во всех направлениях волновое колебание некой невесомой, невидимой и вездесущей материальной среды, названной «эфиром». Виднейшими физиками, развивавшими волновую модель, были Гюйгенс и, позднее, Френель. Волновая теория отлично объясняла такие известные в оптике явления, как дифракция, интерференция и преломление света на границе двух сред.
Чтобы исторический перечень был полным, нужно еще добавить, что чуть ранее существовала еще одна модель, предложенная Декартом. И по этой модели, свет на любые расстояния передается мгновенно, подобно передаче давления в некой абсолютно жесткой среде. Декарт и придумал название этой среде – «эфир». Однако вскоре, в астрономических наблюдениях Ремера, о которых мы еще поговорим, выяснилось, что свет имеет хоть и огромную, но, все же, конечную скорость. И модель Декарта умерла. Но понятие «эфира» перекочевало в волновую модель, которая в нем тоже нуждалась, и прожило там еще долгую и богатую приключениями жизнь.
Обе модели света, и корпускулярная и волновая, имели очень существенные изъяны. Корпускулярная модель не могла толком объяснить явления дифракции и интерференции. А главной проблемой волновой теории стал «эфир», загадочная и неуловимая субстанция, переносящая на себе световые волны, – ведь в механической модели для распространения волновых возмущений необходима материальная среда, реальная, обладающая какими-то физическими свойствами. А «эфир» оставался пустой выдумкой, призраком, лишенным всяческих свойств. Кроме этого, у волновой модели были поначалу трудности с объяснением прямолинейности световых лучей, и с объяснением явлений поляризации.
Однако во второй половине 19 века произошла революция в физике: Фарадеем и Максвеллом была раскрыта взаимосвязь магнитных и электрических явлений.
Максвеллом была создана стройная и всеобъемлющая, подкрепленная точными и красивыми математическими формулами, теория электродинамики, непогрешимая по сей день, проверенная тысячекратно в расчетах и экспериментах. Максвелл предсказал, на основе своей теории, существование электромагнитных волн, и он же предположил, на основании очень близкого совпадения предсказанной им скорости распространения электромагнитных волн и экспериментально найденной скорости света, что свет представляет собой не что иное, как электромагнитные колебания. Оба предсказания блестяще подтвердились на практике – в опытах Герца и опыте Винера. В рамках электродинамики Максвелла получали объяснение все известные явления оптики, включая поляризацию и прямолинейное распространение света. Волновая модель торжествовала убедительную победу, корпускулярная модель была всеми отвергнута и списана в архив.
Триумф волновой теории омрачала лишь одна деталь – было совсем не похоже, чтобы свет и другие электромагнитные волны нуждались для своего распространения в какой-то вещественной «проводящей» среде – они прекрасно преодолевали и космическое пространство, и глубокий вакуум. Загадочный «эфир», среда распространения электромагнитных волн, – оставался непонятым и неуловимым.
История двух моделей света будет неполной, если я не скажу о том, что корпускулярная модель не долго пылилась на полках. В 1905 году она снова оказалась полезной для объяснения явления фотоэффекта, и возродил ее к жизни никто иной, как главный герой этого рассказа, Альберт Эйнштейн. Работа Эйнштейна, посвященная фотоэффекту, стала первым толчком к созданию целого нового раздела физики – квантовой физики. Но это уже совсем другая история.
Откровенно говоря, мы совсем не должны углубляться в изучение оптики или электродинамики – это только отвлечет нас от главной цели. Из многочисленных свойств и параметров света нас в СТО будет интересовать один единственный – скорость его распространения. И я привел здесь краткую историю двух представлений о свете только потому, что в них совершенно по-разному должна определяться скорость света относительно произвольно выбранного наблюдателя.
Согласно корпускулярной модели, источник света как бы «выстреливает» частички света – фотоны, подобно тому, как ружье выстреливает пули, а пушка снаряды. Благодаря такой аналогии корпускулярная модель света получила еще одно название – баллистическая модель. Скорость частиц относительно источника света остается в баллистической модели постоянной, независимо от того, куда и с какой скоростью движется источник. Действительно, ружье выбрасывает пули всегда с одинаковой скоростью, согласно своим паспортным данным (допустим, 500 м/сек), независимо от того стоит стрелок на земле или мчится на гоночном автомобиле. Мы оставим без объяснения тот факт, что одинаковая скорость вылета пули бывает только у одного и того же ружья, а у разных моделей ружей она разная. Если бы аналогия была полной, то свет от столь разных источников, как свеча, дуговая лампа, и, скажем, солнце, имел бы самую разную скорость относительно источника. Но эксперименты этого не обнаруживают. Спишем этот вопиющий факт на несовершенство баллистической модели, но отвергать ее, только на этом основании, не станем.
Итак, по баллистической модели, – скорость света в системе отсчета, привязанной к источнику света, всегда остается постоянной. Можем коротко называть ее скоростью испускания света. А скорость света в любой другой, произвольно выбранной системе отсчета будет складываться из скорости испускания света источником и скорости движения самого источника, в полном соответствии с преобразованием координат Галилея. Точно так же, как скорость снаряда, выстреленного из пушки летящего военного самолета, с точки зрения наземного наблюдателя, будет суммой скорости снаряда относительно пушки и скорости самолета относительно земли. Иными словами:
В баллистической модели скорость света относительно произвольно выбранного наблюдателя должна зависеть от скорости источника относительно наблюдателя.
В волновой модели все происходит иначе – скорость распространения волн определяется исключительно свойствами материальной среды, в которой они распространяются, ну и, разумеется, скоростью наблюдателя относительно этой среды; и совершенно не зависит от скорости источника света. Вспомните круги на воде, возникающие от падения брошенного Вами камня: разве скорость разбегания этих кругов зависит от скорости и направления падения камня? Конечно же, нет! В этом примере камень служит источником волнового возмущения. Можно привести другой пример: если Вы станете водить по поверхности воды прутиком, то скорость волн, вызванных Вами, никак не будет зависеть от скорости перемещения прутика, хотя прутик и будет их источником. То же самое можно сказать и о звуке – механических колебаниях воздуха. Скорость звука относительно воздуха постоянна, независимо от того, куда движется источник звука.
Согласно волновой модели, скорость света относительно произвольно выбранного наблюдателя никак не зависит от скорости источника света, но зависит от скорости наблюдателя относительно «эфира» – среды, в которой распространяется свет.
Скорость испускания света (вспомним, что так мы назвали скорость света относительно источника), которая в баллистической модели была величиной постоянной, в волновой модели становится зависящей от скорости источника относительно «эфира».
Обратите внимание, что в рамках волновой модели, появляется особая, привилегированная система отсчета – та, которая привязана к «эфиру». Только в этой «избранной» системе отсчета, свет распространяется с одинаковой скоростью во всех направлениях. В любой другой системе, наблюдатель должен будет обнаружить неравномерность распространения света – свет будет двигаться с разной скоростью в разных направлениях. Это подрывает важный принцип относительности, принятый в классической физике, согласно которому все инерциальные системы отсчета равноправны и все физические законы имеют в них одинаковый вид.
В заключение этой главы, позвольте привести еще одну простую иллюстрацию, наглядно отражающую разницу между двумя предложенными моделями, баллистической и волновой. На основе этого примера, Вы сможете решить, если только захотите, сторонником какой из моделей Вы являетесь.
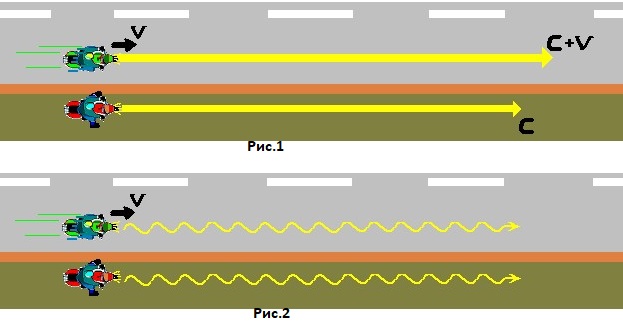
На рисунке ниже изображены два мотоциклиста: один стоит неподвижно на обочине шоссе, второй едет по тому же шоссе со скоростью «v». Предположим, что в тот момент, когда второй мотоциклист оказывается точно рядом с первым, оба они одновременно включают дальний свет фар. Вопрос: будут ли лучи света обоих мотоциклов продвигаться вперед с одинаковой скоростью?
Если Вам кажется, что луч второго мотоцикла обгонит луч первого, как показано на рис.1, то Вы сторонник баллистической модели. А если считаете, что оба луча помчатся вперед с равной быстротой, как изображено на рис.2, то Вас, согласно дорелятивистским представлениям, надо записать в сторонники «эфира» и волновой модели.
Следует, однако, подчеркнуть, что, несмотря на все отличия волновой и баллистической модели, есть одна важная деталь, которая их объединяет: с позиций классической физики, в обеих моделях скорость света зависит от выбора наблюдателя; для обеих может существовать такой наблюдатель, относительно которого скорость луча света будет равной нулю, и даже отрицательной. В отношении последнего примера с мотоциклистами, это означает, что всегда существует такой быстрый «третий» мотоциклист, пусть и воображаемый, который сможет догнать свет фар, как первого, так и второго мотоциклов.
Глава 6. Постоянство скорости света

(не Эйнштейн, как кто-нибудь мог подумать)
Теория относительности постулирует постоянство скорости света в любой инерциальной системе отсчета. Постулирует – значит, не доказывает, а принимает это утверждение как аксиому, отправную точку для дальнейших построений и расчетов. Очевидно, что никакая серьезная физическая теория не может постулировать что-то, что расходится с накопленным практическим опытом и результатами экспериментов.
В этом все и дело, что накопленный к началу ХХ века опыт говорил о постоянстве скорости света для любого наблюдателя, покоящегося в любой ИСО, и этот опыт вопиющим образом противоречил основам классической физики, точнее, элементарному кинематическому правилу сложения скоростей при переходе из одной СО в другую, – всем знакомому по школе преобразованию Галилея.
Эйнштейн принял постоянство скорости света, установленное из опыта, за исходное условие своей теории, и показал, что на основании этого условия можно выстроить непротиворечивую физическую картину мира, в которую войдут все известные ранее физические законы, скорректированные с учетом нового, уже не галилеевского, преобразования координат.
Чтобы обрести уверенность в справедливости СТО, очень важно глубоко обдумать и принять результаты тех опытов, в которых было выявлено постоянство скорости света. Противники СТО, критикуя Эйнштейна, очень часто строят свои возражения именно на несогласии с постулатом постоянства скорости света, не вполне понимая, что они, тем самым, спорят не с Эйнштейном, а с результатами сотен экспериментов, предшествовавших появлению СТО, не говоря об огромном числе тончайших экспериментов, проведенных после, уже для её проверки. Поэтому мы обязательно должны, хотя бы вкратце, ознакомится с историей измерения скорости света, а также с наблюдениями и опытами, подтвердившими ее неизменность в любых системах отсчета.
Но прежде приведем одно рассуждение, наводящее на мысль о постоянстве скорости света, хотя доказательствам, строго говоря, оно служить не может. Как-то на вопрос «что послужило толчком к созданию СТО?», Эйнштейн образно ответил: «Меня занимала мысленная погоня за лучом света».
Давайте и мы с вами, по примеру Эйнштейна, попробуем мысленно догнать световой луч. С точки зрения классической физики, это вполне реально – ведь скорость материальных тел в ней ничем не ограничена. И если скорость света конечна, то никакой проблемы в том, чтобы его догнать, нет. Ну, по крайней мере, теоретически нет. Так вот, представим себя на минуту таким наблюдателем, которому удалось разогнаться настолько, что он догнал луч света и летит рядом с ним. И даже не просто рядом с ним, а рядом с самым его кончиком.
Что же мы увидим? А мы увидим удивительную вещь – стоящий неподвижно световой луч, застывшее электромагнитное колебание, не способное продвинутся в пространстве ни на миллиметр дальше той точки, где расположился наблюдатель. Может быть, если вы не очень хорошо знакомы с электромагнитными явлениями, эта картина и не покажется вам странной. Но с точки зрения физика, уверяю вас, трудно придумать что-либо более дикое, чем неподвижная электромагнитная волна. Электромагнитные колебания представляют собой процесс распространения в пространстве двух взаимосвязанных и синфазно меняющихся полей – вихревого электрического и вихревого магнитного. Эти поля могут существовать только в движении, постоянно поддерживая друг друга – изменение одного из них порождает другое, и наоборот. Причем, изменения их носят колебательный, гармонический характер. Математически все это описывается знаменитыми уравнениями электродинамики Максвелла. Уравнения Максвелла требуют знаний высшей математики, и поэтому мы их не рассматриваем (Как вы помните, мы с вами стараемся избегать формул). Но в этих уравнениях присутствует некая константа «С», физический смысл которой нас очень интересует: она имеет размерность скорости, и обозначает скорость распространения электромагнитного возмущения. И решение уравнений Максвелла однозначно требует, чтобы электромагнитные колебания не стояли на месте, а передавались все дальше и дальше в определенном направлении с постоянной скоростью «С». Разумеется, свет и другие электромагнитные колебания можно поглотить или отразить, поместив на их пути препятствие (экран, зеркало). Однако, при наличии пустого пространства по пути следования луча, электромагнитная волна, согласно уравнениям электродинамики, остановиться не может.
И вот что примечательно – тот факт, что в уравнениях Максвелла величина, имеющая смысл скорости распространения света, представлена константой, а не переменной, зависящей от выбора системы отсчета, делает их неинвариантными к классическому преобразованию координат Галилея. Уравнения Максвелла, с точки зрения классической физики, попросту не являются универсальными – они могут быть точны только в одной единственной системе отсчета, – той, которая неподвижна относительно «эфира».
Чтобы сделать их универсальными и пригодными к использованию в любой другой системе отсчета, требовалось, казалось бы, совсем немногое: явным образом ввести в теорию понятие «эфира», и скорректировать уравнения с учетом скорости движения выбранной системы отсчета относительно «эфира». Максвелл, несомненно, все это понимал. И хотя он, похоже, искренне верил в существование эфира, но корректировать свои уравнения все-таки не стал. Возможно, не захотел вносить в свою теорию нечто странное, не обнаруженное ни в каких предшествующих опытах.
Так или иначе, в том, что великий физик оставил свои формулы без изменений – с постоянной скоростью света, – было нечто провидческое. Может быть, правы были современники Максвелла, говорившие, что «рукой его двигал сам бог».
Глава 7. Астрономические наблюдения Ремера
(Из истории измерений скорости света; первое пришествие эффекта Доплера)
Первое в истории экспериментальное доказательство конечности скорости света – заслуга датского ученого Олафа Ремера (1644-1710). Ремер с 1671 года работал в Париже, в обсерватории, руководимой Жан-Доменико Кассини, и проводил анализ наблюдений за спутником Юпитера Ио (одним из четырех крупнейших спутников Юпитера, открытых Галилеем в 1610 году). В наблюдениях обнаруживалось странное нарушение периодичности вращения спутника вокруг Юпитера, которое удивительным образом было связано с годичным движением Земли вокруг Солнца.
Не во всякой литературе, посвященной измерениям скорости света, приводится детальное описание этих наблюдений и сделанных Ремером выводов. К сожалению, мне приходилось встречать как ошибочное толкование их, так и спекулятивные попытки представить полученные Ремером данные, как противоречащие СТО. Так что мы задержимся на выводах Ремера чуть подольше.
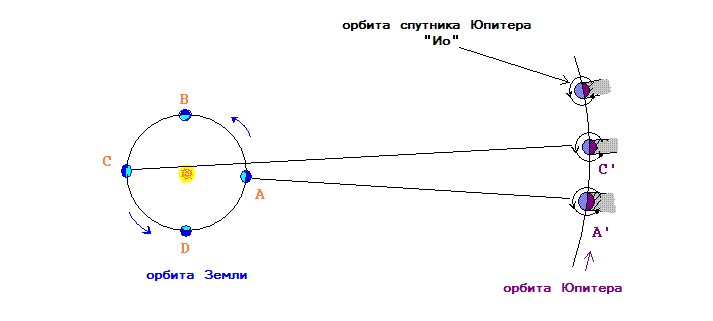
Итак, на руках у Ремера были составленные в ходе многолетних методичных наблюдений таблицы, определяющие время захода Ио в тень гиганта Юпитера. Вращение планет и их спутников – очень устойчивый и равномерный процесс, и потому затмения спутника Юпитера должны наступать с практически идеальной периодичностью. Никакого заметного физического (гравитационного и пр.) влияния на этот процесс маленькая и далекая Земля оказать не может. И, тем не менее, при наблюдениях с Земли на протяжении одного земного года обнаружились колебания ритма затмений Ио Юпитером. Чтобы понять, что же заметили астрономы 17-го века, взгляните на рисунок в начале главы:
На рисунке показана орбита Земли и кусочек орбиты Юпитера. Земля, в ходе своего годичного движения вокруг Солнца, последовательно проходит точки «А», «B», «C», «D», и возвращается в «А». Юпитер же, за это время, преодолевает лишь небольшую часть своей орбиты (полный юпитерианский год равен примерно 12-ти земным годам). Предположим, что мы начали наблюдения в точке «А» – Юпитер в этот момент находился в точке «А’». По астрономической терминологии этот момент называется «противостоянием» Юпитера (имеется в виду, что, с точки зрения земного наблюдателя, он противостоит Солнцу). Допустим, исключительно для облегчения нашей задачи, что период обращений Ио вокруг Юпитера, равен в точности 24 часам. Это не соответствует реальности, но зато чудо как удобно для демонстрации: это означает, что, если сегодня Ио скрылся в тени Юпитера ровно в девять вечера, то и назавтра его заход произойдет ровно в 9:00, и послезавтра тоже, и после-после…и т.д.
– Ну и что же? – спросите вы.
А то, что эта замечательная точность сохраняется лишь неделю-другую, пока Земля еще вблизи точки «А». Затем вы вдруг начнете замечать, что хронометрическая идиллия закончилась, и с каждым днем Ио все больше отстает от 24-часового графика – сначала на секунды, затем на 1, 2,…5 минут. И когда Земля приблизится к точке «B», заход Ио будет происходить уже не в девять ровно, а в 9ч:10мин, и с каждым днем он будет запаздывать еще на 10-12 секунд.
Через полгода с начала наблюдений, когда Земля достигнет точки «С», а Юпитер – точки «C’», отставание от первоначального графика составит приблизительно 20 минут, заход Ио будет наблюдаться теперь в 9ч:20мин. Однако отставание больше не будет нарастать, время каждого оборота Ио вокруг Юпитера снова станет равным совершенно точно 24 часам.
С этого момента все происходит как бы в обратном порядке – стремительный бег Ио вокруг Юпитера вначале незаметно, а затем все более отчетливо, опережает 24-часовой ритм, и когда Земля возвращается в точку «А», заход Ио в тень Юпитера снова происходит ровно в 9:00 вечера.
Ремер проанализировал все накопленные данные – разумеется, реальная картина была посложнее, чем в нашем примере, т.к. время оборота Ио вокруг Юпитера составляет не 24 часа, а примерно 1.77 земных суток, – и сделал важный вывод:
Запаздывание заходов Ио, нарастающее в течение полугода, за время движения Земли от точки «А» к точке «С», и достигающее примерно 20 минут в точке «С», может быть объяснено увеличением расстояния от Юпитера до Земли и конечностью скорости света. Когда Земля расположена в точке «А», расстояние от Земли до Юпитера минимально, когда Земля в точке «С» – расстояние максимально. Разница между этими расстояниями равна, приблизительно, диаметру земной орбиты (Сравните отрезки [AA’] и [CC’] на рис.1). По мере того, как Земля перемещается из «А» в «В», и затем в точку «С», свету, идущему от спутника Юпитера, приходится преодолевать все большее расстояние до земного наблюдателя. Если бы свет распространялся мгновенно, то изменение расстояния до Земли не играло бы никакой роли. Но если скорость света конечна, тогда наблюдаемое запаздывание времени захода Ио, безусловно, должно быть объяснено этой разницей расстояний.
Существует и другая интерпретация наблюдений Ремера, дополняющая первую. Эта вторая интерпретация акцентирует внимание на ситуации, возникающей при прохождении Землей точек «В» и «D». Расстояние, которое проходит свет от Юпитера до этих точек, примерно одинаково, но в точке «В» наблюдается замедленное вращение спутника Юпитера, а в точке «D», наоборот, ускоренное. Это заключение совершенно логично, и находится в полном согласии с нашим (и Ремера) предыдущим выводом. Действительно, как иначе может накапливаться интегральная разница в 20 минут между точками «А» и «С», если не будет замедления в точке «В», и последующего ускорения в точке «D».
Постойте-ка, – а не кажется ли вам, что подобное явление нам уже знакомо?
Мы ведь его совсем недавно обсудили, и довольно подробно. Ну, припоминайте-припоминайте: наблюдатель приближается к источнику сигнала – частота сигнала увеличивается, наблюдатель удаляется – частота сигнала падает. Что это?
Ну, конечно, – это же эффект Доплера в его световом, оптическом варианте! Источником светового периодического сигнала является вращающийся вокруг Юпитера спутник Ио, наблюдатель находится на Земле, и, ведя свои наблюдения в точке «В», он удаляется от источника сигнала, а в точке «D» – приближается к нему. Когда земной наблюдатель удаляется от Юпитера, интервал между наблюдаемыми затмениями спутника возрастает, то есть, частота сигналов уменьшается. А когда он движется навстречу Юпитеру, интервал между затмениями сокращается – частота сигналов возрастает.
Выходит, что Ремер и другие астрономы столкнулись с доплер-эффектом еще в 17-м веке. По этой причине, в некоторых статьях о наблюдениях Ремера, можно встретить утверждение, что честь открытия эффекта Доплера на самом деле принадлежит Ремеру, который обнаружил этот эффект для световых лучей задолго до того, как Доплер открыл подобный эффект для звуковых колебаний. Авторы этих статей иногда даже предлагают переименовать эффект Доплера в «эффект Ремера». Должны ли мы согласиться с ними?
Вопрос спорный: есть доводы «за», есть и «против». Как мы видели, возможны две интерпретации наблюдений Ремера: одна, основанная на разнице расстояний до Юпитера в точках «А» и «С» земной орбиты, и другая, основанная на доплер-эффекте в точках «В» и «D». Первую можно назвать «интегральной», а вторую – «дифференциальной», хотя они являют собой две стороны одной медали. Если бы Ремер использовал чисто интегральный подход, то навряд ли мог бы считаться первооткрывателем эффекта Доплера. Однако более детальное знакомство с историческими фактами убеждает, что Ремер отчетливо понимал оба возможных подхода, и их взаимосвязь.
Теоретическое объяснение, которое он поначалу приводит для рассмотренного явления, основано как раз на втором подходе – сравнительном анализе наблюдений в точках «В» и «D», то есть на удлинении/укорочении одного цикла обращения спутника, при движении Земли к Юпитеру либо от него.
Однако на практике зафиксировать это небольшое отклонение имеющимися в то время в распоряжении астрономов приборами оказалось затруднительно. Ремера это не обескураживает, он без труда переходит к «интегральной» картине явления:
“То, что незаметно для двух обращений, становиться весьма значительным для многих, взятых вместе” – пишет он. Именно суммарное отклонение времени захода спутника, накопленное за полгода движения Земли по орбите, дает Ремеру основания уверенно говорить о конечности скорости света, несмотря на то, что многие современники (и в том числе его прямой руководитель Кассини) с недоверием отнеслись к его сообщению.
Так что же, возвращаясь к вопросу об авторстве, – пора переименовать эффект Доплера в эффект Ремера? Не думаю. Я совсем недавно узнал, что существует такой полусерьёзный закон одного чикагского профессора (закон Стиглера), который гласит:
“Ни одно научное открытие не носит имени своего первооткрывателя.”
Помимо этого, есть еще одно существенное обстоятельство: классический эффект Доплера рассматривает распространение волнового процесса в «проводящей среде». Он оперирует понятиями длины волны, скорости источника, скорости наблюдателя и скорости сигнала относительно среды.
А теперь обратим внимание на то, как Ремер строит свою «дифференциальную» интерпретацию. Она, по методу построения, идентична «интегральной» интерпретации. В обоих случаях наблюдаемый эффект объясняется одной единственной общей причиной – изменением расстояния от наблюдателя до Юпитера. Об изменении скорости сигнала относительно наблюдателя в ней и речи нет – выводы Ремера логичны и при постоянстве скорости света относительно Земли в точках B и D.
И, что еще существеннее, – у Ремера нет и тени упоминания о «эфире», среде распространения света, относительно которой надо определять скорость сигнала.
Такой подход очень верен именно для света и для объяснения релятивистского доплер-эффекта. И не случайно мы выбрали подобную формулировку – через изменение расстояния между источником сигнала и наблюдателем, – для первого знакомства с эффектом Доплера. Но в классической интерпретации эффекта Доплера эта формулировка является неполной, незавершенной и недостаточной для выполнения точных вычислений.
Так что, много логичнее называть «эффектом Ремера» именно релятивистский эффект Доплера, а классический оставить под прежним названием. При этом, как мне кажется, мы ничуть не умаляем заслуг замечательного датского астронома – для своего времени он сделал огромный шаг вперед, преодолевая, к тому же, немалое сопротивление своих коллег.
Ремер вполне мог вычислить, основываясь на предполагаемом диаметре земной орбиты, первое в истории науки экспериментальное значение скорости света. Может, он и проделал это вычисление, однако не опубликовал его, не будучи уверен, что диаметр земной орбиты достаточно точно определен. Надо еще принять во внимание, что большинство подлинных рукописей Ремера не дошло до наших дней, многие документы сгорели в Парижской обсерватории при пожаре 1728г. Величину скорости света, на основании наблюдений Ремера, вычислили позднее другие ученые. Ошибка в полученном ими результате была связана исключительно с неточным знанием параметров земной орбиты. Если бы во времена Ремера диаметр орбиты Земли мог быть достоверно измерен, он получил бы потрясающе точный результат для скорости света, превосходящий результаты многих более поздних опытов.
Глава 8. Брэдли объясняет явление звёздной аберрации.
(Из истории измерений скорости света; Джеймс Брэдли)

Несмотря на открытие Ремера, конечность скорости света еще сравнительно долгое время оставалась для физиков предметом разногласий. И только в 1727 году английский астроном Джеймс Брэдли поставил точку в этом споре, объяснив явление аберрации света (от лат. aberratio — отклонение) при годичном наблюдении за звездами.
Звёздной аберрацией света называют небольшое изменение угла, под которым свет далеких звезд попадает в телескопы земных наблюдателей, происходящее вследствие движения Земли по орбите вокруг Солнца.
В отличие от встреченного нами ранее эффекта Доплера, который можно было рассматривать скалярно – т.е., для источника сигнала и наблюдателя, движущихся вдоль одной оси, – аберрация света является пространственным, векторным эффектом. Она возникает, если наблюдатель меняет направление движения относительно источника света, и перемена скорости происходит не вдоль прямой, ведущей к источнику, а под углом к ней. Наиболее сильно выражена аберрация света, когда наблюдатель начинает движение под прямым углом к направлению лучей, идущих к нему от источника света.
(Это явление не следует путать с явлениями хроматической и сферической аберрации, о которых вы, возможно, слышали. И хроматическая и сферическая аберрация связана с определенными конструктивными недостатками оптических приборов, и не имеет никакого отношения к теме этой главы.)
Одна из наиболее наглядных и точных аналогий, которая обычно приводится для иллюстрации явления аберрации, – это аналогия с человеком, бегающим под струями дождя. Когда человек стоит на месте, то, в отсутствие ветра, он видит дождь падающим вертикально вниз. Но стоит ему начать двигаться, как струи дождя наклоняются, и ему кажется, что дождь льет наискосок. Тот, кто смотрит на дождь из окна быстро едущего автомобиля или поезда, видит струи дождя очень сильно наклоненными, почти горизонтальными. И если стоящий человек при такой погоде держит зонтик прямо над головой, то идущий пешеход, чтобы не промокнуть, вынужден будет держать зонтик немного впереди себя. Взгляните на рисунок: дождь на нем идёт строго вертикально для стоящего человека, но для каждого из шагающих рядом человечков струи дождя выглядят наклонными, причем наклон зависит от того, куда кто движется.
Поток света, приходящий к нам от любой из звезд на небосводе, подобен струям дождя – звезды так далеки, что все лучи от одной звезды, падающие на Землю, практически параллельны друг другу. И подобно тому, как бегающему по кругу человеку будет казаться, что дождь все время меняет свое направление, так бег Земли по орбите приводит к тому, что свет от всех практически звезд приходит к земному наблюдателю под меняющимся углом, отличным от истинного угла, под которым каждая из звезд расположена на небесной сфере. Угол, на который отклоняются дождевые струи, определяется соотношением двух векторов – скорости падения капель и скорости движения человека. А угол отклонения лучей света при аберрации определяется векторным отношением скорости светового луча и скорости движения Земли вокруг Солнца. И, если бы скорость света была бесконечной, то явления аберрации света отсутствовало бы.
Сам Брэдли так пишет о своем открытии: “Наконец я догадался, что если свет распространяется во времени, то кажущееся положение неподвижного предмета, когда глаз находится в покое, будет иное, чем когда глаз движется в направлении, уклоняющемся от линии, соединяющей предмет с глазом, и что когда глаз движется в различных направлениях, то и кажущееся положение объекта будет различным”.
Никаких формул для расчета угла аберрации я приводить не стану. Сразу оговорюсь, что точные математические операции сложения векторов скоростей, равных или сравнимых со скоростью света, нельзя производить по законам классической евклидовой геометрии. Их можно делать, только с учетом пространственных преобразований Лоренца и, очень желательно, поняв перед этим специальную теорию относительности, чем, собственно, мы и заняты.
Но представить себе порядок отклонения лучей мы можем. Как и раньше с эффектом Доплера, при большой разнице между скоростью наблюдателя и скоростью сигнала, результат вычисления по релятивистской формуле будет очень близок к результату, полученному из треугольника скоростей в простой евклидовой геометрии. Понятно, что угол, на который поворачивается луч света любой звезды из-за движения Земли, невелик, поскольку абсолютное значение скорости Земли всего около 30 км/с, а скорости света – 300000 км в секунду. Согласно астрономическим данным, максимальное значение угла отклонения составляет всего 20,4 угловых секунд, это в случае, когда скорость Земли перпендикуляна направлению на звезду. (Для сравнения – угловой размер Луны и Солнца примерно 30 угловых минут, а Венеры, при максимальном сближении с Землей, – примерно 1 минута.) И, без использования оптических приборов, годичные колебания положения звезд на небе никогда не были бы замечены.
Однако, для мощных астрономических телескопов 20 секунд – очень заметный угол. Главное зеркало телескопа (рефлектора, разумеется) подобно перевернутому зонтику, только, в отличие от зонтика, оно не рассеивает поток света, а, отражая параллельные лучи, собирает их снова в яркую точку – изображение звезды. Если лучи строго параллельны трубе телескопа, то изображение звезды окажется точно в фокусе, в центре поля зрения телескопа, на его «оптической оси». Если же лучи падают наклонно на главное зеркало, то изображение звезды будет смещено от оптической оси, и если мы, скажем, фотографируем эту звезду на фотопластинку, размещенную точно в центре фокальной плоскости телескопа, то изображение звезды окажется сдвинутым от центра пластины.

Заметим, что наблюдение аберрации затруднено тем обстоятельством, что Земля еще и вертится вокруг своей оси. И это приводит к тому, что звезды все время движутся по небу по окружностям, параллельным земному экватору. Окончательное положение звезд на небе есть результат сочетания этих двух движений Земли – вращения вокруг своей оси и перемещения по орбите. Но вращение Земли вокруг оси не вносит никакой погрешности в звездную карту: звезды сохраняют свое неизменное положение друг относительно друга и относительно двух главных плоскостей небесной сферы – плоскости экватора и эклиптики. А вот движение Земли по орбите и вызванная им аберрация – искажают карту звезд. Суточное вращение можно полностью компенсировать с помощью точного механического привода, поворачивающего телескоп в направлении, противоположном вращению Земли. Такой часовой привод будет постоянно удерживать в поле зрения телескопа один и тот же участок звездного неба, и если мы продолжим наблюдать в течение года за звездами с помощью такого телескопа, то сможем увидеть постепенное смещение звезд, вызванное аберрацией.
Мы увидим, что за год звезды как бы описывают маленькие круги вокруг тех точек, где им полагается быть согласно звездным атласам. И только если бы однажды движение Земли вокруг Солнца остановилось, мы увидели бы звезды точно в тех местах, где они показаны в звездных картах.
Глава 9. Проверка механических моделей. Крах баллистической модели
Наш экскурс в историю открытий несколько затянулся, и я чувствую, как нетерпеливый читатель уже пролистывает страницы, говоря: «Ну зачем мне все эти старые наблюдения, которые доказывают всего лишь конечность скорости света. Это я знаю сам. Давай уже вернёмся к СТО, ты ведь обещал предъявить доказательства неизменности скорости света относительно любого наблюдателя».
Ну, во-первых, я думаю, что вся история открытий, связанных со светом, достаточно интересна, и мы ничуть не пожалеем о том, что подробней познакомились с ней.
Во-вторых, я в свое время наслушался немало упрямых, начитанных, но не слишком вдумчивых людей, стремящихся опровергнуть Теорию Относительности; и они часто отталкивались в рассуждениях (всегда ошибочных, заметим) как раз от этих, очень старых наблюдений Ремера и Брэдли, не умея их правильно интерпретировать. Для наблюдений Ремера, они используют только ту часть классической формулы доплер-эффекта, где изменение частоты завит от скорости сигнала относительно наблюдателя, и “забывают” про ту ее часть, которая определяет совершенно аналогичное изменение частоты с изменением расстояния, не говоря уже о том, что действитеьно точное значение дает только релятивистская формула (просто разница между тремя этими результатами на несколько порядков меньше предельной точности измерений Ремера). Для наблюдений Бредли, они пытаются доказать, что наклон лучей меняться вследствие оптического преломления лучей в околоземном “слое эфира”, что эфир увлекает и наклоняет лучи, не понимая, что этот наклон – элементарный кинематический эффект, при переходе наблюдателя с другую систему координат. Они подобны человеку, увязывающему наклон линий дождя с обязательным наличием воздуха и ветра. Однако, если бы дождь шел в безвоздушном пространстве, они убедились бы, что линии дождя точно также наклоняются для наблюдателя в машине или поезде, хотя никакого воздуха и ветра нет.
А, в-третьих, дорогие читатели, я только что в предыдущей главе допустил оплошность, но Вы её, вероятно, не заметили. И если не заметили, то еще недостаточно прониклись идеей относительности и равноправия ИСО, и её противникам несложно будет сбить Вас с пути истинного. Я написал, что, вследствие движения Земли по орбите, звёзды видны «под меняющимся углом, отличным от ИСТИННОГО угла, под которым каждая из звезд расположена на небесной сфере». Вы должны были остановить меня возгласом:
– Как «истинного»? Разве есть «истинный угол»? Не хочешь ли ты, автор, сказать,
что существует одна-единственная, истинно неподвижная СО, в которой все звёзды неподвижны? И только в ней все направления и траектории лучей света – истинные, а в остальных – искаженные?
Нет же. Конечно, нет! То, что я назвал «истинным» положением звёзд – всего лишь направления на них в ИСО Солнца, которое мы принимаем за точку начала отсчета. Но и Солнце, и все соседние звёзды движутся относительно друг друга. И вместе они движутся вокруг центра Галактики (с немалой скоростью, замечу). И галактики движутся одна относительно другой в кластере галактик. И никакого «истинно» неподвижного центра этого движения указать невозможно. Если бы притяжение Солнца внезапно исчезло, и Земля продолжила движение по прямой, то Землю можно было бы считать условно неподвижной, а направления на звёзды, наблюдаемые в этот момент, больше не менялись бы, и стали бы для нас «истинными» (не дай бог, конечно). Я, со временем, выделю свой ответ критикам СТО, ссылающимся на наблюдения Ремера и Брэдли, в отдельную главку…
Что ж, пора заняться демонстрацией постоянства скорости света в любой ИСО. Именно демонстрацией, а не математическим доказательством, потому что это постоянство – следствие наблюдений и логики, а не математических выкладок. Что мы имеем?
Мы имеем две механических модели движения света (электромагнитных волн): баллистическую и волновую.
Согласно обеим моделям, обязательно существует, хотя бы в теории, такой наблюдатель, который может догнать или обогнать луч света. Согласно обеим – скорость света непременно должна зависеть от выбора системы отсчета, или, что одно и то же, от выбора конкретного наблюдателя. Но только в первом случае – на скорость света должна влиять относительная скорость источника света и наблюдателя, а во втором – скорость наблюдателя относительно «эфира». В соответствии с этим заключением мы и будем в дальнейшем подыскивать схемы экспериментов, которые могут на практике подтвердить или опровергнуть каждую из моделей.
Достаточно очевидно, что никакой «гибридной» механической модели света придумать невозможно, а, если и возможно, то это будет такая причудливая смесь бульдога с носорогом, что обсуждать её всерьёз я не берусь. Поэтому, либо-либо: либо поток частичек, свободнее всего чувствующий себя в пустоте (баллистическая модель), либо волны, бегущие в невидимой и невесомой среде (волновая модель).
Начнем с баллистической модели. Баллистическая модель полагает, что скорость света относительно источника света постоянна. В ней есть множество недочетов и странностей. Во-первых, странно, что скорость излучения всеми источниками одинакова. Ведь даже револьверы разных марок имеют разную начальную скорость пули. Почему свет, идущий от свечи, дуговой лампы, от лазера, и от Солнца – все имеют одну начальную скорость? Но на практике ведь это именно так. Во-вторых, как может быть, что всевозможные прозрачные среды, хоть и уменьшают скорость света в них, но внутри среды скорость света остается неизменной на всей траектории? Если среда замедляет, то должна и дальше тормозить. А свет только тускнеет, но движется с одной неизменной скоростью. Где постепенное замедление, вплоть до остановки, которое неизбежно происходило бы с механическим частицами, попавшими в тормозящую среду?
Всё же, мы не станем с порога отвергать эту модель. Баллистическая модель хороша тем, что в ней нет никакой выделенной системы координат, и она полностью удовлетворяет принципу относительности. Скорость света в любой СО, не связанной с источником, должна складываться из скорости света относительно источника и скорости самого источника света. Когда, в рамках этой модели, мы говорим о скорости источника света, ясно, что имеется в виду скорость источника относительно наблюдателя.
Понятно, что никакие опыты, в которых источник света и приёмник жестко закреплены на неизменном расстоянии в этом случае непригодны. Нам нужны опыты, в которых источник двигался бы с разной скоростью относительно приемника(наблюдателя), а расстояние, проходимое светом в СО наблюдателя, было бы в точности известным, а лучше — просто одинаковым, и достаточно большим, чтобы разница в скорости приводила к большой разнице во времени прихода сигнала. Тогда мы сможем сравнить скорость сигнала напрямую, без всяких ухищрений и косвенных измерений по частоте через «доплер».
Простой гипотетический пример подобного опыта: два космических аппарата, летящих навстречу, вдоль одной линии: один – от Земли, второй к Земле, т.е., один удаляется, другой приближается. Когда они поравняются, аппараты должны одновременно послать сигнал на Землю. Если сигнал того аппарата, который летит к Земле, придёт первым, а сигнал второго, удаляющегося, запоздает — тогда баллистическая модель имеет право на жизнь. Ну, что, знатоки? Как думаете? Вряд ли кто усомнится, что сигналы придут одновременно… Правда, это гипотетический опыт, хотя и возможный при сегодняшнем уровне техники.
К счастью, надобности в нем нет, ибо сам космос дает практически бесконечное количество возможностей для похожих наблюдений — все те далекие объекты, которые вращаются — двойные звезды, планеты у других звёзд, вращающиеся галактики, — представляют собой светящиеся тела, которые, в процессе вращения, движутся то к Земле, то от Земли. Подходит и спутник Юпитера Ио, о котором мы говорили в главе про наблюдения Ремера. Если бы верна была баллистическая модель, то каждый оборот Ио вокруг Юпитера, наблюдаемый с Земли, был бы неравномерен: пол-оборота, когда он движется к Земле, пролетали бы быстрее на час или два, чем пол-оборота в направлении от Земли. А для более далеких объектов, например, планет у других звезд, происходили бы совсем фантастические вещи — одну и ту же планету мы видели бы одновременно в противоположных местах орбиты, часть изображений двигались бы в правильном направлении, другая часть – задом наперед.
Все взрывы сверхновых мы видели бы растянутыми на сотни лет — сначала только ту часть разлетающейся материи, которая направлена была к Земле, потом ту, которая разлетается по бокам, и наконец, еще долгие годы в инфракрасном свете, ту часть светящейся материи взрыва, которая полетела от Земли.
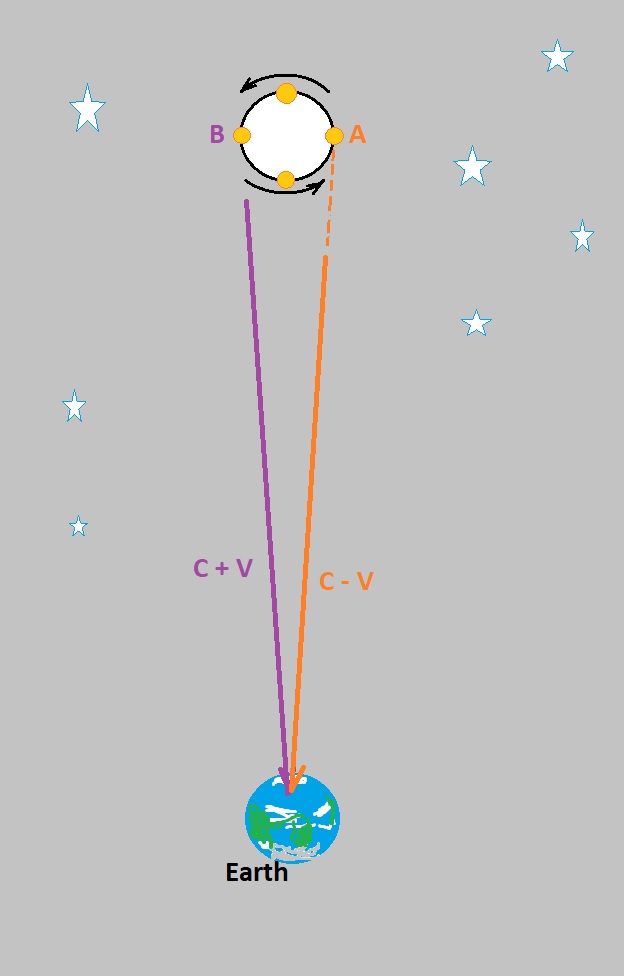
Посмотрите на рисунок. На нем показано некое вращающееся со скоростью V тело (пусть звезда, вращающаяся вокруг другой звезды или черной дыры), очень далекое от нас, и наша Земля, с которой мы за ним наблюдаем. Звезда, в процессе вращения, находится попеременно то в точке «А», то в точке «В». Но свет, по баллистической модели, из точки «А» летит к Земле со скоростью (C-V), а из точки «В» со скоростью (C+V). И, естественно, если расстояние до Земли большое (а так оно и есть), то свет от точки «В» догоняет, и перегоняет (может быть, на несколько оборотов по времени) свет от точки «А».
На рисунке, для примера: свет от точки «В» в точности догнал свет от точки «А», значит, земной наблюдатель должен одномоментно видеть звезду в двух противоположных точках орбиты.
В общем, полнейшая ерунда эта баллистическая модель, в свете современных знаний. Все астрономические наблюдения, которым нет числа, опровергают её начисто, и, напротив, подтверждают равную скорость света с любого направления, и от любых источников, к земному наблюдателю. И не только света, но и радиоволн, разумеется.
Глава 10. Проверка волновой модели. Крах модели “эфира”
Перейдем теперь к волновой модели, согласно которой всё космическое пространство заполнено некой невидимой, невесомой, всепроникающей материей, которая, сама по себе, абсолютно необнаружима, про свойства которой неизвестно ничего, кроме одного – она является средой распространения электромагнитных волн. И именно относительно этой среды («эфира») свет распространяется с постоянной скоростью во всех направлениях (изотропно). А во всех прочих СО – нет.
Эта модель сложнее и солиднее баллистической. В ее рамках находят объяснение многие оптические явления. В ее базовой форме, она предполагает, что «эфир» однороден и более-мене неподвижен в той единственной СО, относительно которой свет распространяется изотропно.
Существуют попытки представить «эфир» неким газом, который то полностью увлекается телами, то частично увлекается, то проникает в тела, то не проникает, и, соответственно, образует «слои», «потоки», «завихрения», и обладает «плотностью», «вязкостью» и пр. Соответственно, его поведение должно описываться зубодробительными дифференциальными уравнениями, наподобие уравнений газодинамики, при том, что ни одна из характеристик эфира никому не ведома (их предполагается каждый раз подгонять под желаемый результат). Братцы, да СТО кристально чиста, логична, проста, с её единственным, математически несложным, преобразованием координат, в сравнении с этим навороченным безумием!
Поэтому мы пожелаем сторонникам «эфирной гидро- и аэродинамики» успеха на их тернистом пути, и распрощаемся навсегда, потому что оттуда не возвращаются. И займемся проверкой базисной эфирной теории. У этой теории есть несколько замечательных преимуществ, в плане опытной её проверки:
Во-первых, нам не нужно, чтобы источник и приёмник двигались относительно друг друга (как для баллистической модели). Они могут быть соединены в единую жесткую конструкцию, разделенные очень точно измеренным расстоянием, и вместе с этой конструкцией передвигаться относительно «эфира». При разной скорости и разном угле поворота установки по отношению к эфиру – еще говорят, при разной скорости «эфирного ветра», – время прохода сигнала от источника к приемнику непременно должно изменяться. Вторым замечательным преимуществом, вытекающим из первого, является то, что никакого искажения частоты сигнала, связанного с эффектом Доплера, в такой конструкции не может случится никогда, ни в каком положении! Потому что эффект Доплера – всегда результат разности скоростей источника сигнала и приемника (советую обдумать это утверждение, очень полезно…). Третьим замечательным преимуществом, вытекающим из двух предыдущих, является то, что изменение скорости прохождения сигнала – на заданном расстоянии и при неизменной частоте, – выразится строго однозначно в изменении фазы сигнала, достигшего приёмника. А уж сдвиг фазы сигнала мы умеем измерять с поразительной точностью. Поэтому и длина опытной установки, чтобы заметить сдвиг фазы, не должна быть слишком большой.
Догадайтесь, как называется прибор, использующий для точного обнаружения разности фаз явление интерференции? Правильно, интерферометр (как Вы догадались?!). Нет, не обязательно Майкельсона. В принципе достаточно одной трубки, по которой когерентный (лучше всего – лазерный) луч пробежит сначала в одну сторону – от источника до зеркала, затем обратно, и уже возле источника наложится на луч, вылетающий из источника, для получения интерференционной картинки. Но двухплечевой интерферометр – как у Майкельсона,- чтобы проверять за один раз два направления, конечно, и того лучше. На практике, любой интерферометр (и одноплечевой, и двухплечевой) приходится поворачивать, чтобы засечь, как изменяется, или не изменяется, интерференционная картинка.
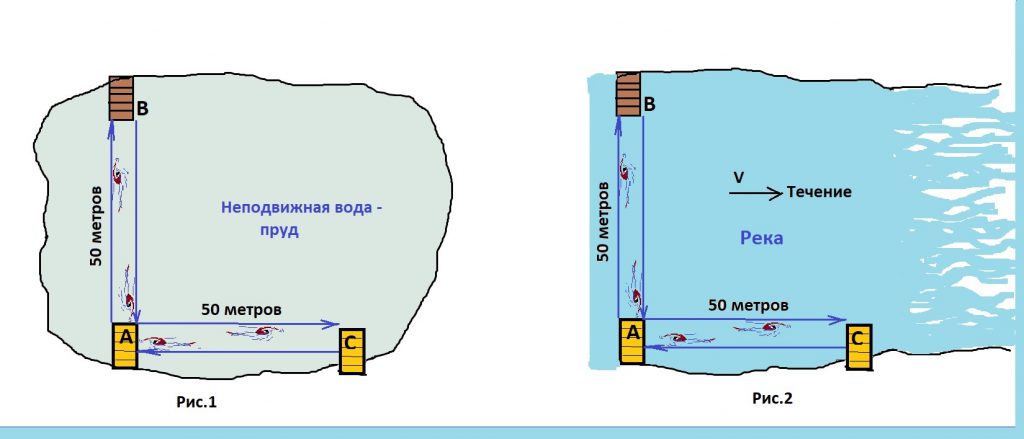
Картинки, объясняющие принцип проверки времени прохождения сигнала по разнице фаз, приведены на примере пловца, переплывающего либо неподвижный пруд (рис.1), либо реку (рис.2).
На пруду не важно, поплывёт пловец от мостков «А» к мосткам «В» и обратно, или от мостков «А» к мосткам «С» и обратно: в обоих случаях, он проплывет расстояние в 100м, и, если один полный гребок его равен точно 1 метру, он закончит обе дистанции точно под конец сотого гребка (с вытянутой вперед рукой).
А на реке обе дистанции пловец проплывёт за разное время, и оно, в обоих случаях, будет большим, чем в неподвижной воде. (- На сколько именно? Пожалуйста, считайте сами… я обхожусь, как видите, без вычислений, одним только качественным объяснением.) Соответственно, пловец закончит дистанцию на разной фазе гребка.
В этом суть опыта Майкельсона, и множества других подобных, значительно более точных опытов, в которых так и не удалось обнаружить «поток эфирного ветра».
Главным итогом всех измерений и проверок скорости света является то, что свет не желает подчиняться классическому правилу сложения скоростей. Скорость света грубо нарушает закон «преобразования координат» Галилея, являющийся одним из краеугольных камней старой физики, и остается постоянной при переходе из одной системы отсчета в другую. И из осознания этого факта вырастает Специальная Теория Относительности.
Глава 11. Объяснение СТО. Исходная позиция
Упрямое постоянство скорости света как относительно источника излучения, так и относительно любого наблюдателя, немедленно приводит к неразрешимому противоречию, потрясающему до основания всё здание классической физики, и ведущему к неизбежному пересмотру традиционных представлений о пространстве и времени. Здание, надо сказать, устояло, но перебралось на обновлённый фундамент. Мне не раз вспомнилось, пока я обдумывал эту книжку, что одна из известных научно-популярных книг Даниила Данина называется «Неизбежность странного мира». Книга эта посвящена, в большей мере, истории развития квантовой физики, но заглавие её как нельзя лучше подходит и к Теории Относительности Эйнштейна. Все, что мы обсудили до сих пор, было только введением в Специальную Теорию Относительности. Сейчас мы переходим к самому ее существу.
Для начала, постараемся выстроить простую и наглядную иллюстрацию того неразрешимого противоречия, о котором только что говорили.
Возьмем две воображаемых очень длинных, прямых и твердых доски, наподобие школьной линейки, только больше. Подравняем их заранее, чтобы они были абсолютно одинаковой длины, положим, 10 метров каждая (а можно и 100, или километр). Поставим на каждой доске метку точно посередине, или, еще лучше, нанесём на них с помощью эталона длины мерные деления, в точности, как это делают на обычных линейках. Теперь попробуем решить следующую техническую задачу:
Мы собираемся в дальнейшем расположить наши доски-линейки строго параллельно, на небольшом расстоянии друг от друга, и перемещать одну вдоль другой (как показано на рисунке 1). Нам нужно, чтобы в тот момент, когда концы линеек окажутся точно друг напротив друга, на концах линеек происходила вспышка света, или включалась лампочка.
Одно из возможных решений таково – на концах линеек укрепить металлические стержни и зарядить их противоположными зарядами, так чтобы между остриями стержней, при их сближении, проскакивала искра (рис.2).
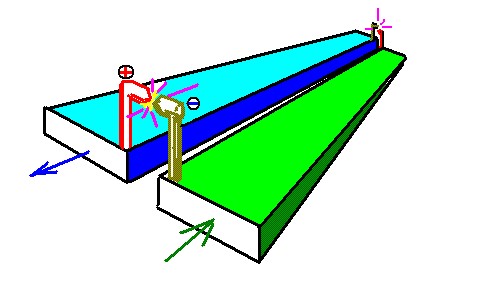
Метод с искрой хорош еще тем, что источник света в нем не привязан жестко ни к одной из сторон, и это делает обе линейки, даже по отношению к источникам света, совершенно равноправными. Очень возможно, что предыдущие главы не окончательно убедили вас в постоянстве скорости распространения света, и вам будет казаться, что размещение источника на определенной доске превратит ее в привилегированную систему отсчета и повлияет на результаты дальнейших опытов. Признаюсь, что мне и самому это ошибочное рассуждение долгое время мешало воспринимать некоторые популярные иллюстрации к теории относительности. В этом случае, исключительно для простоты и ясности восприятия, вариант с искрой между двух стержней является предпочтительным.
Теперь разместим в середине каждой линейки по наблюдателю: в середине синей линейки (назовем ее «А») поставим наблюдателя «А», а в середине зеленой линейки (линейка «В») поставим наблюдателя «В». Затем, возьмем и утащим эти линейки вместе с наблюдателями далеко-далеко в космос, подальше от Земли и даже от Солнечной системы, благо заботиться о пропитании и жизнеобеспечении воображаемых участников эксперимента нам не нужно. И там, в глубоком космосе, вдали от Солнца и других привычных ориентиров, вначале разведем линейки на некоторое расстояние, а затем толкнем их навстречу друг другу параллельными курсами, так, чтобы они пролетели рядышком, точно, как показано на рис.1 и рис.2.
Зачем нам понадобилось проводить мысленный эксперимент так далеко от Земли? Это нужно для того, чтобы две рассматриваемые системы отсчета предстали перед нами абсолютно равноправными, инерциальными, безо всяких оговорок, свободными от воздействия внешних сил и посторонних материальных тел. Мне важно, чтобы читатель (и даже ярый сторонник «эфира»), глядя на иллюстрации, мог с равной легкостью представить себе неподвижным любого из наблюдателей.
СТО не так-то легко объяснять с помощью рисунков. Я уже отмечал, что у меня, при первых попытках изучить теорию относительности, возникали трудности с восприятием иллюстраций: встреченные мной в книгах рисунки, призванные быть опорой для понимания, казались недостаточно четкими и убедительными. На типовых иллюстрациях, одного из наблюдателей обычно изображают стоящим на земле – на перроне железнодорожной станции или на берегу реки, а второго помещают в движущийся мимо вагон или на плывущую баржу. Вспышки света происходят или в небе – от молний, сверкающих вообще непонятно где, – либо в концах вагона или баржи. Для большей достоверности картины художники часто добавляют еще и живописные окрестности, которые, правду сказать, больше мешают, чем помогают. Довольно трудно абстрагироваться от деталей, и представить обе изображенные системы отсчета равноправными. И, кроме того, – «отягощенному» знанием начал астрономии читателю нелегко принять за «инерциальную систему отсчета» баржу, плывущую по шарообразной поверхности Земли, которая, при этом, вращается вокруг своей оси, да еще и вращается вокруг Солнца, которое… и т.д.
Но, мы отвлеклись. Давайте же вернемся к предстоящему опыту. В ходе нашего воображаемого эксперимента, мы потребуем строгого выполнения двух условий:
1. Картина происходящих событий, в описании каждого из двух наблюдателей, должна быть абсолютно идентичной, «симметричной», и не должна давать никаких оснований считать одну из линеек, и связанную с ней систему отсчета, чем-то особенной и отличной от других. В частности, каждый из наблюдателей, с абсолютно равными основаниями, может считать себя неподвижным.
2. Постоянство скорости света во всех инерциальных системах отсчета. То есть, в нашем примере, скорость света должна быть одинакова относительно каждого из наблюдателей, любой из линеек, и в любом направлении (а интересующих нас направлений будет всего два).
Эти два условия, собственно, и представляют собой два главных постулата, положенных в основу СТО: второе условие основано, как мы уже говорили, на накопленных в физике экспериментальных данных, а первое – это сам его Величество «принцип относительности», или, иначе, принцип равноправия инерциальных систем отсчета.
Итак, взглянем на наших наблюдателей, стоящих в серединах своих досок. На рис.3 показано то самое положение, которое нам изначально хотелось получить: летящие в пустоте доски-линейки поравнялись друг с другом, а стоящие на них наблюдатели очутились буквально лицом к лицу.

В этот момент между заряженными стержнями на обоих концах должна проскочить искра, и свет от вспышек помчится во все стороны, в том числе, и в сторону наблюдателей. Голубая и зеленая стрелки показывают относительные направления движения каждой из линеек. Однако, понятно, что обозначение это достаточно условное, и каждая линейка может с равными основаниями считаться неподвижной. Каждый из наблюдателей, с позиций классической физики, имеет право утверждать, что свет с обеих сторон придет к нему одновременно, ибо он стоит точно посередине между вспышками и считает себя неподвижным. А сами вспышки обязаны произойти одновременно – ведь доски-то абсолютно одинаковой длины.
Но, с точки зрения элементарной логики, никак не может быть, чтобы они оба оказались правы! Если вспышки, как мы полагаем, происходят одновременно, и наблюдатели в момент вспышки находятся точно друг против друга, то, за время прохождения лучей, наблюдатели успеют разлететься на некоторое расстояние. Так что, еще можно предположить одновременность прихода лучей к одному из них, но никак не к обоим. Если до одного из них свет справа и слева и вправду дойдет одновременно, то и второй наблюдатель это подтвердит, ибо два луча высветят первого наблюдателя одновременно с двух сторон. Одновременность достижения двумя лучами одного из наблюдателей будет неоспоримой, ибо тут мы имеем дело с одновременностью событий в одной точке пространства. В этом случае, очевидно, что до второго наблюдателя лучи дойдут не одновременно, и эта неодновременность тоже будет абсолютной и заметной первому наблюдателю.
Не будем ограничиваться одним только словесным комментарием и продолжим рисовать. На следующих рисунках показано, как должны развиваться события, по мнению каждого из наблюдателей (напомню, что «сознание» воображаемых наблюдателей остается пока в рамках классической физики). Точка зрения наблюдателя «А» представлена на рис.4:

Наблюдатель «А», разумеется, считает неподвижными себя и свою линейку, а линейку «В» движущейся, поэтому, ждет одновременного прихода к нему обоих лучей. Этот момент как раз и изображен на рисунке. Наблюдатель «А» резонно полагает, что второй наблюдатель к этому времени будет освещен только наполовину – справа, как и показано на рисунке, – так как луч левой вспышки еще не успел до него добраться. Естественно, что сам наблюдатель «В» не сможет, в таком случае, отрицать, что вначале он был освещен справа, и лишь потом – слева.
Проблема, однако, в том, что наблюдатель «В» представляет себе все наоборот – так, как показано на рис.5:
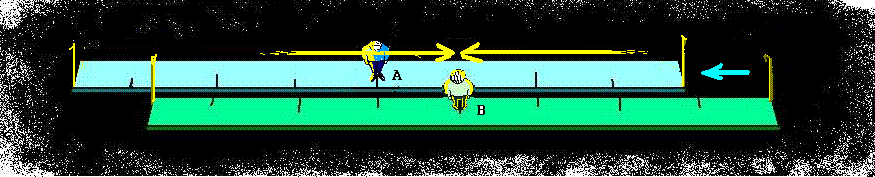
Он полагает свою линейку «В» неподвижной, и считает, что свет вспышек осветит одновременно как раз его, а до наблюдателя «А» дойдет неодновременно. И не видит никаких оснований принимать точку зрения своего «оппонента». Кто же из двоих наблюдателей окажется прав?
Глава 12. Объяснение СТО. Варианты
Давайте, выразим возможные результаты нашего опыта в простой и четкой логической форме. У нас есть два исходных предположения:
• Лучи света достигнут одновременно наблюдателя «А» (это предположение наблюдателя «А»),
• Лучи света достигнут одновременно наблюдателя «В» (предположение наблюдателя «В»).
И, отсюда, согласно формальной логике, всего четыре возможных результата:
1. Оба утверждения правильны.
2. Прав наблюдатель «А» («В» ошибается).
3. Прав наблюдатель «В» («А» ошибается).
4. Оба наблюдателя неправы.
Сразу же ясно одно: исходные утверждения – взаимоисключающие, поэтому, первый из четырех вариантов мы отметаем.
«Ну, что ты тянешь! – возмущается нетерпеливый читатель, – Давно уже ясно, что оба неправы! Берем четвертый вариант!». О да, ты прав, догадливый читатель. В конечном счете, верен именно четвертый вариант. Но, прошу, давайте еще какое-то время не будем исключать из рассмотрения варианты «2» и «3». С их помощью, нам будет легче сделать некое очень важное промежуточное заключение. Итак, отбросив пока только один из возможных результатов, и оставив остальные три, мы смело можем утверждать следующее: в противоречивой ситуации, которую мы смоделировали, по крайней мере, один из наблюдателей обязательно констатирует неодновременность прихода к нему световых сигналов. Не имея возможности объяснить ее разностью скорости сигналов (пункт 2 наших основных условий – второй постулат – запрещает ему это!), он будет вынужден сделать вывод о неодновременности вспышек света.
В ясном понимании этого факта – ключ к пониманию всей СТО.
Сделаем небольшое отступление. Обратим внимание на одну очень важную деталь в возникающей проблеме одновременности двух событий: противоречие возникает только для событий, произошедших в двух разных, удаленных друг от друга точках. Возникает оно из-за того, что заключение об их одновременности каждый наблюдатель делает после получения информации о событиях, в нашем случае – после получения световых сигналов. И фиксация одновременности (либо неодновременности) событий осуществляется наблюдателем с задержкой, вызванной запаздыванием сигнала.
Для событий, происходящих в одном месте, понятие одновременности является абсолютным и бесспорным. Так, если бы наблюдатели на линейках, очутившись друг против друга, оба протянули руку и хлопнули друг друга по плечу то, естественно, этот хлопок был бы одновременным для них самих, и для любого другого наблюдателя. Хотите еще пример? Если Вы, гуляя по лесу, решили съесть яблоко, и, откусывая яблоко, споткнулись и упали (извините!), то эти два события – откусывание яблока и падение – являются одновременными как для Вас, так и для любого наблюдателя, даже если он летит над лесом в ракете. Вам не понравилось, что Вы упали, да еще на виду у наблюдателей? Хорошо, сейчас исправим… Итак, Вы с приятелем шли по лесу, и собрались съесть яблоко. И ровно в тот момент, когда Вы принялись за яблоко, Ваш приятель споткнулся и упал. Так лучше? И снова, откусывание яблока, и падение Вашего товарища – события одновременные для любого наблюдателя, независимо от того, куда и с какой скоростью он движется. И только в случае, когда Вы откусываете яблоко в одном месте, а Ваш товарищ, в поисках грибов удалившийся в лес, спотыкается и падает в другом месте, в километре от Вас, установление одновременности этих событий вызовет ту сложность и путаницу, которая показана в нашем абстрактном, умозрительном примере с линейками.
Вернемся к нашему воображаемому опыту с линейками.
Что получается? Если какой-то из наблюдателей прав, и обе вспышки для него будут выглядеть одновременными, то для другого они обязательно окажутся неодновременными. Мы приходим к довольно странному и даже шокирующему выводу, с которым, поначалу, нашему интуитивному сознанию трудно смириться:
События, происходящие в двух разных местах и одновременные, с точки зрения одного из наблюдателей, явятся неодновременными для другого, движущегося относительно первого с постоянной скоростью, и наоборот – то, что одновременно для второго, не одновременно для первого.
Для нас это только промежуточный вывод, т.к. мы еще не закончили разбираться с нашим примером, и все еще хотим понять, что же все-таки произойдет с наблюдателями и линейками на самом деле. Но, в то же время, задержимся на секунду и почтительно приподнимем шляпы, ибо это важнейший и фундаментальный принцип СТО, отменяющей прежнее единство мирового времени, и, вместе с ним, такое казалось бы первичное и незыблемое понятие, как одновременность. Одновременность удаленных в пространстве событий – относительна! Она зависит от выбора системы отсчета, точно так же, как зависит от нее наблюдаемая скорость тел.
Глава 13. Объяснение СТО. Длина тел
Вернемся к решению задачки с наблюдателями «А» и «В», стоящими на линейках. Мы уже поняли, что свет до обоих не может дойти одновременно. Теперь самое время вспомнить о первом постулате ТО – полном равноправии инерциальных систем отсчета. Из оставшихся трех вариантов решения, те два, в которых лучи доходят до одного из наблюдателей одновременно, а до другого нет, обладают очевидным недостатком – они нарушают симметрию. А принцип равноправия систем отсчета в нашем случае требует именно абсолютной симметрии – т.е., картина происходящего для первого и второго наблюдателя должна быть полностью идентична. Наблюдатели никоим образом не должны почувствовать, что один из них находится в особом, избранном положении, позволяющим считать его «истинно неподвижным», а другого «движущимся». Принцип относительности допускает лишь относительное движение, каждый наблюдатель с полным правом может считать свою систему координат покоящейся. И поэтому, нам остается единственный вариант ответа – свет до обоих наблюдателей дойдет неодновременно. Он и есть верный.
В первую минуту покажется, что все еще есть лазейка для спасения наших старых представлений о пространстве. Ну, конечно, лучи света не дойдут одновременно до наблюдателей, стоящих посередине своих линеек. Но лучи же должны встретиться в некоторой средней точке, между разъехавшимися наблюдателями? Да, конечно, точно между ними. Вот до этой-то «особой точки» лучи справа и слева дойдут одновременно. И картина будет симметричной для обоих наблюдателей… и снова можно будет заявить об «абсолютной одновременности» вспышек…
Стоп! Стоп, дорогой читатель. Неужели Вы уже забыли, о чем мы так долго толковали в прошлых главах? Ай-я-яй! А как же наш второй постулат – принцип постоянства скорости света для любого наблюдателя!? Неужели мы готовы отказаться от него при первых же трудностях? А ведь мы сейчас фактически подумали о том, что лучи полетят к наблюдателям с разной скоростью – тот, что идет с правой стороны относительно каждого наблюдателя, помчится быстрее (как будто «навстречу»), а тот, что слева – медленнее (как бы «вдогонку»). И придумали «особую точку», относительно которой свет распространяется с равной скоростью. И к какой же системе координат, интересно, привязана эта точка – «А» или «В»? Нет, не к ним… Уж не к тому ли листу бумаги, на котором мы чертим рисунки, и относительно которого теперь считаем обе линейки движущимися? Так забудьте о нем! Нет его, мы с Вами в пустом космическом пространстве, которое неподвижно относительно обоих наблюдателей.
Чувствуете, что происходит? Мы сейчас, в попытке разрешить парадокс, придумали третью, промежуточную систему отсчета, в которой лучи движутся с одинаковой скоростью, и встречаются точно посередине между вспышками, но лишили системы “А” и “В” права на изотропность и постоянство скорости света. Совсем не к этому мы стремились, не такую картину должны были получить, руководствуясь постулатом постоянства скорости света. Это путь обратно в тупик, из которого мы хотели вырваться!
Пустое пространство – это не экран монитора или лист бумаги, на котором мы рисуем; оно не вещественная среда, которая покоится только в одной ИСО. Оно “покоится” в любой выбранной нами инерциальной СО. В этом и состоит истинный принцип равноправия, это и есть физическая суть относительности. Именно с этим так не хочет смириться наш, так называемый, «здравый смысл».
А потому, отступим на шаг назад, поставим себя на место одного из наблюдателей, и задумаемся снова:
Итак, свет пришел к нам неодновременно. Мы стоим точно в середине линейки (этот факт мы не подвергаем пересмотру). Свет справа и слева идет к нам с абсолютно одинаковой скоростью, согласно 2-му постулату. Остается только одно объяснение неодновременности – свет дошел неодновременно, потому что неодновременными были сами породившие его вспышки.
Но как такое могло быть!? Что за чудеса! Ведь линейки были одинаковой длины, а концы двух одинаковых параллельных линейеек могут поравняться только одновременно! «Были одинаковой длины» … БЫЛИ… но остались ли? Вот в чем вопрос!
Догадываетесь, к чему дело клонится? Ах, бедный мой читатель, только что тебя вынудили отказаться от единого времени и понятия одновременности. И тут же требуют новых жертв. Теперь требуется пожертвовать единством и неизменностью длин. Но она неизбежна, эта новая жертва – две линейки, движущиеся одна вдоль другой, почему-то стали неодинаковыми, по крайней мере, с точки зрения наших наблюдателей.
Оказывается, не только невозможно установить единое время для двух пространственно удаленных событий, вдобавок придется признать, что один и тот же предмет имеет разную длину, в зависимости от того, из какой системы отсчета мы его наблюдаем. Только отказавшись как от абсолютного мирового времени, так и от абсолютных (одинаковых для всех наблюдателей) длин и расстояний, можно отыскать единственно верный, логически непротиворечивый переход из одной системы в другую, обеспечивающий выполнение обоих постулатов СТО – переход, выражаемый математическими формулами Лоренца с такой обманчивой простотой.
Однако нам еще нужно ответить на вопрос: окажется движущаяся линейка короче или длиннее, чем «неподвижная» – та, на которой находится наблюдатель? Надо просто описать логическую цепь событий для обоих вариантов, и мы поймём, какой из них согласуется для наблюдателей, а какой нет. Предположим, что движущаяся линейка выглядит короче, чем неподвижная (именно к такому выводу и приводит СТО, в чем мы скоро убедимся), и попробуем составить картину происходящего глазами наблюдателей «А» и «Б».
Относительно наблюдателя «А», движущейся является линейка «В», и значит, с его точки зрения, именно она окажется короче. А с точки зрения наблюдателя «В», более короткой окажется линейка «А». Поначалу можно подумать, что тут какая-то логическая неувязка: как так – и та «короче», и эта «короче»? Все потому, что мы привыкли длину, и вместе с ней понятия «короче», «длиннее», считать абсолютными. Однако, они относительны. Мы не должны ни на секунду забывать, что принцип равноправия двух наблюдателей требует полной симметрии, полного подобия в описании ими происходящих событий. И уж если для первого наблюдателя «своя» линейка окажется длиннее, чем «чужая», то и для второго картина должна быть аналогичной. Именно в том и заключается относительность длин, что каждый из наблюдателей имеет свое, равноправное представление о длине предметов.
Итак, выслушаем сначала наблюдателя «А» и постараемся изобразить на рисунке его рассказ. Его описание событий будет таким:
«Когда движущаяся линейка «В» поравнялась со мной, оказалась, что она стала короче (как бы сжалась в продольном направлении). Поэтому сначала задний по ходу ее движения (левый по отношению к наблюдателю «В») край линейки «В», соприкоснулся с контактом на правом конце моей линейки, от этого произошла первая вспышка – справа от меня. Затем, через некоторое время, передний, по ходу ее движения, (правый по отношению к наблюдателю «В») конец линейки «В» достиг левого края моей линейки, и тогда произошла вторая вспышка – слева от меня. Естественно, что свет справа, от первой вспышки, достиг меня первым, а свет слева, от второй вспышки, – дошел вторым. Но до наблюдателя «В» вначале дошел свет от второй вспышки (справа от него), потому что он двигался ей навстречу, и уже потом его догнал свет от первой вспышки».
Свой рассказ наблюдатель «А» мог бы сопроводить таким рисунком (Рис.1):
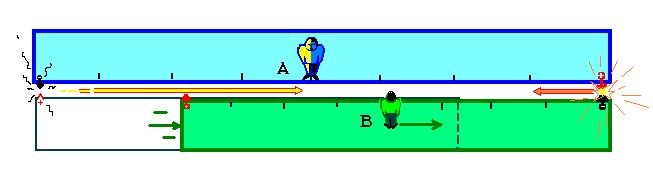
А вот рассказ наблюдателя «В»:
«Когда движущаяся линейка «А» поравнялась со мной, оказалась, что она стала короче (как бы сжалась в продольном направлении). Поэтому сначала задний по ходу ее движения (левый по отношению к наблюдателю «А») край линейки «А» соприкоснулся с контактом на правом конце моей линейки, от этого произошла первая вспышка – справа от меня. Затем, через некоторое время, передний, по ходу ее движения, (правый по отношению к наблюдателю «А») край линейки «А» достиг левого края моей линейки, и тогда произошла вторая вспышка – слева от меня. Естественно, что свет справа, от первой вспышки, достиг меня первым, а свет слева, от второй вспышки, – дошел вторым. Но до наблюдателя «А» вначале дошел свет от второй вспышки (справа от него), потому что он двигался ей навстречу, и уже потом его догнал свет от первой вспышки» (Рис.2).
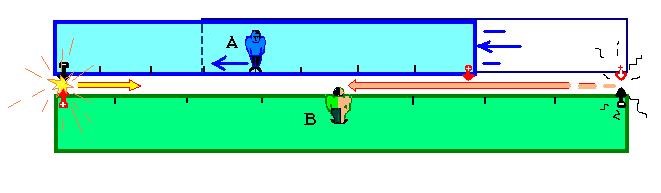
Как видите, рассказы полностью идентичны, они переходят один в другой простой подменой «А» и «В». И в них царит полное согласие относительно того, в каком порядке свет приходит к каждому из наблюдателей. Но не следует все же забывать о двух важных расхождениях между ними:
– Наблюдатель «А» полагает уменьшившейся в длине линейку «В». Наблюдатель «В», наоборот, – линейку «А».
– Вспышка, которую наблюдатель «А» называет «первой», для наблюдателя «В» – «вторая», и наоборот. Порядок вспышек оказывается для них противоположным.
Из-за этих расхождений нам пришлось – впервые в этом повествовании – рисовать не одну, а две картинки, чтобы показать, как одни и те же события выглядят глазами двух разных наблюдателей. Помните, в главе про эффект Доплера я говорил, что рисунок, сделанный с точки зрения одного наблюдателя, содержит правдивую, но неполную, информацию, и что, для полноты картины, нам не хватает рисунка, который мог бы сделать другой наблюдатель (тогда им был космонавт в ракете). Теперь нам придется частенько рисовать по два рисунка, вместо одного, чтобы представить точную картину происходящего в разных системах координат.
А что, если движущаяся линейка показалась бы наблюдателям не короче, а длиннее? Я предоставлю вам самим провести мысленное сопоставление событий в этом случае… Согласуются события? – Нет, не согласуются! В этом случае наблюдатели приходят к непримиримому противоречию относительно того, в каком порядке к каждому из них должен прийти свет от вспышек.
Почему же противоречия, касающиеся длины линеек и последовательности вспышек, мы считаем примиримыми, а противоречие, касающееся порядка прихода лучей к любому наблюдателю, непримиримым? – спросят любознательные читатели. Дело в том, что в реальном мире нарушение последовательности событий, происходящих с конкретным материальным телом, совершенно невозможно, это нарушило бы важнейший принцип причинности – принцип, который в теории относительности соблюдается неукоснительно.
В теории относительности происходит много странного – искажение размеров и расстояний, замедление хода времени, – но нарушения логической, причинно-следственной цепи событий не происходит никогда, какую бы систему координат мы ни выбирали для наблюдений. Различный порядок следования может быть только у событий, пространственно удаленных друг от друга, и являющихся причинно-независимыми (неспособными влиять одно на другое) – как в случае со вспышками на концах линеек. Но последовательность событий, происходящих с любым из наблюдателей, должна в любой системе отсчета быть одинаковой – именно такой, какой она была для самого наблюдателя. Все события, происходящие во времени с любым материальным объектом, потенциально являются причинно-зависимыми. Поясню: можно зарядить револьвер и затем выстрелить, сорвать грушу и затем съесть ее, прочесть письмо и затем сжечь его. Но нельзя проделать эти действия в противоположном порядке: выстрелить из револьвера прежде, чем он будет заряжен; вначале съесть грушу, а потом сорвать ее; сжечь письмо, а затем прочесть его.
С наблюдателями тоже легко смоделировать ситуацию, когда разная последовательность прихода лучей к одному наблюдателю приведет к разным последствиям, – достаточно договориться, что каждый наблюдатель должен сесть, если он будет раньше освещен справа, или остаться стоять, если раньше окажется освещенным слева. Понятно, что физическая реальность не может «раздвоиться», как в фантастических фильмах.
Хочу заметить: тот факт, что на движущейся мимо линейке часы идут иначе, чем на собственной неподвижной, не только не мешает, но даже помогает нам примириться с тем, что длина этой линейки будет в нашей системе иной, чем длина покоящейся линейки. О том, как именно идут часы, мы поговорим ниже (и дело не в «быстрее-медленней», все немного хитрее).
Глава 14. Объяснение СТО. Пространство-время
Я должен сразу успокоить Вас, дорогие читатели. Никакого силового сжатия, никакой реальной деформации движущейся линейки, конечно же, не происходит. Мы ни на секунду не должны забывать, что, с точки зрения находящегося на ней наблюдателя, его линейка покоится, и длина ее неизменна.
– А, ну вот! – радостно воскликнет скептик, – я же говорил, это кажущееся сокращение длины. Всё дело в том, что, когда движущийся предмет наблюдают или фотографируют, то свет от переднего и заднего края движущегося предмета приходит с разной задержкой. Поэтому наблюдателям кажется, что он короче. Мы лишь видим его коротким, а на самом деле его длина та же, что была. А Вы устроили из этого такой шум!
Не совсем так, дорогой читатель. Да, сократившуюся длину движущегося предмета можно назвать «кажущейся», но не в обычном смысле. Если бы на концах каждой линейки (из предыдущей главы) стояли наблюдатели с часами, идущими точно и синхронно с часами наблюдателя, стоящего посередине, и фиксировали бы момент совпадения концов линеек без всякой задержки, они все равно зафиксировали бы разное время. Я чуть забегаю вперед, но дальше Вам станет понятен смысл следующей формулировки:
Сократившаяся длина не является кажущейся, потому что движущийся предмет в любой момент времени, действительно, занимает меньшее пространство вдоль той координатной оси, по которой меряет длину наблюдатель, считающийся неподвижным. А «кажущейся» она является в том смысле, что одномоментно зафиксированное положение точек движущегося тела, относится к разным моментам времени по часам «движущегося» наблюдателя. В частности, наблюдая с линейки «А» положение краевых точек линейки «В» (определяющих её длину), мы фиксируем их там, где они оказались одновременно по часам системы «А», но это положение неодновременно по часам системы «В», связанным с движущейся линейкой. Вот почему истинная длина линейки «В» – её обычно называют «собственной длиной» – всегда больше, чем её длина в системе «А». Вспомним промежуточный вывод, сделанный нами в прошлой главе:
События, происходящие в двух разных местах и одновременные, с точки зрения одного из наблюдателей, явятся неодновременными для другого,… и наоборот – то, что одновременно для второго, не одновременно для первого.
Мы впервые приходим здесь к необходимости иметь синхронизированные часы во всех точках выбранной ИСО – именно для того, чтобы исключить задержку на прохождение сигнала. Раньше мы привыкли думать, что на весь космос есть одни часы, которые устраивают всех. Теперь мы поняли, что, раз наблюдатели не могут прийти к единому мнению об одновременности событий, значит, у каждого свои часы. Но как сопоставить их ход? И какой промежуток времени в системе движущегося наблюдателя разделяет те события, которые для неподвижного одновременны? Когда я рисую две разные картинки положения линеек для двух наблюдателей, то каждая из них изображает некое одномоментное положение, с точки зрения одного из наблюдателей. Одномоментное — значит, подразумевается, что во всех точках неподвижной линейки одно и то же время. И, если бы в каждой точке линейки «А» были часы, идущие синхронно с часами наблюдателя «А», они показывали бы одинаковое время.
Но какое время показали бы часы системы «В», если бы на её линейке тоже были часы, расположенные в каждой точке, а не только у наблюдателя «В»? Подумайте совсем немного, и Вы поймете: чем дальше расположены точки событий, одновременных в системе «А», тем больше разрыв во времени, образующийся между этими событиями для наблюдателя «В», – ведь он всё время равномерно удаляется от одной из точек и приближается к другой.
И это означает, что все часы в системе «В», во всех её точках, показывают разное время, с точки зрения наблюдателя «А». Причем, тем более разное, чем дальше они друг от друга (разрыв во времени увеличивается линейно с расстоянием, потому что движение системы «В» линейное и равномерное). Соответственно, все часы системы «А», во всех её точках, показывают разное время, с точки зрения наблюдателя «В».
Мы приходим к еще одному заключению, которое даже более важное, на мой взгляд, чем пресловутое «замедление времени» (до замедления мы тоже вскоре доберёмся) – о том, что каждая точка пространства имеет не только три пространственных координаты, но и координату времени, которая тоже зависит от выбора системы отсчета, и представляет собой локальные (пусть и воображаемые) «часы», синхронизированные с часами в нулевой точке данной СО.
Простейшая процедура синхронизации часов во всех точках пространства как раз основана на том, что у нас имеется сигнал, распространяющийся во всех направлениях с одинаковой скоростью в любой СО, – свет. Следовательно, зная расстояния до всех точек выбранной СО, можно посылать синхронизирующий сигнал от часов, закрепленных в нулевой точке, и, с учетом запаздывания сигнала, выставить часы в любой точке данной СО.
Очевидно, что, если мы пошлем синхронизирующий сигнал из одной «нулевой» точки – оказавшейся общей, на момент посылки сигнала, для двух различных СО, — и продолжим, с приходом этого сигнала, выставлять часы во всех остальных точках этих двух систем, то время на любой оказавшейся рядом (на момент прихода сигнала) паре часов, закрепленных в разных системах, будет выставлено разное. Причем, так было бы даже без эффекта укорочения длин (См. рисунок ниже):
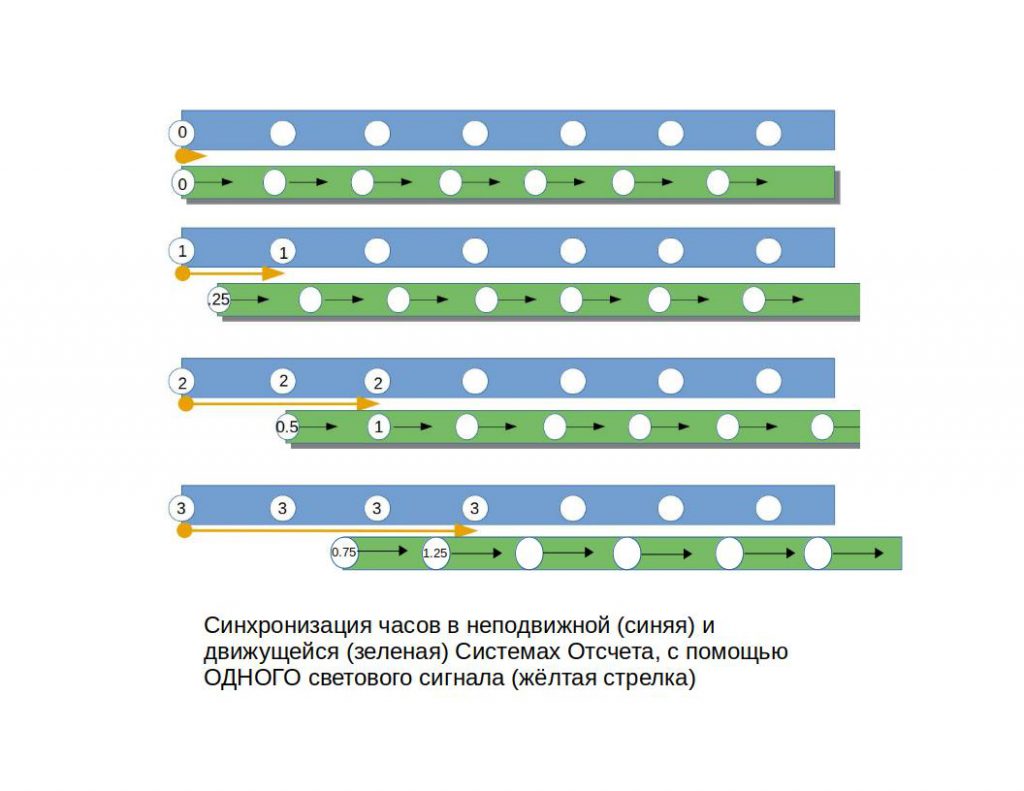
Сделанное выше заключение дает нам ясное понимание того, что мы живем не в трехмерном пространстве с единой для всех временной координатой, но в пространственно-временном континууме, где каждому точечному событию могут быть присвоены не только три координаты, зависящие от выбора системы координат, но и координата времени, тоже зависящая от выбора системы координат. В четырехмерном пространстве-времени, вместо трех-координатной точки, появляется понятие «точки» с тремя пространственными, и одной временной координатами; такая точка и есть – «событие». Два «события» разделены уже не только расстоянием в пространстве, но и «расстоянием» во времени, и такое совокупное пространственно-временное расстояние, разделяющее два события, назвали «интервал между событиями» (или просто Интервал).
Вот Вы сидите, к примеру, у себя на кухне, и кладёте кубик сахара в чай… потом, немного подумав, ещё кубик сахара. Имеются, стало быть, два события: первый и второй кубик, брошенные в чай. Для Вас, в вашей СО, эти два события разделены только временем. Но для лётчика, пролетавшего точно над Вашим домом, когда Вы бросали первый кубик, они разделены и временем (чуть большим, чем для Вас), и расстоянием, потому что между первым и вторым кубиком сахара Вы (в СО, привязанной к самолёту) отдалились.
Метрика пространства-времени такова, что Интервал сохраняется, при переходе из одной ИСО в другую, а трёхмерный вектор расстояния уже нет! Поэтому и линейки у нас сократились.
Глава 15. Замедление времени
Картинка из прошлой главы, иллюстрирует лишь нарастающее (с расстоянием) расхождение часов двух СО, выставляемых по одному световому сигналу. Но она вовсе не служит иллюстрацией замедления часов на движущейся линейке. Многим может даже показаться, что замедлятся только часы, движение которых совпадает с направлением сигнала, а сигнал, направленный в противоположную сторону, навстречу движущимся часам, приведет к тому, что часы эти будут идти с опережением. Неверно! Сигнал, направленный навстречу, приведет к тому, что часы будут выставлены с нарастающим (с ростом расстояния) опережением относительно неподвижных, но это совсем не означает, что они будут идти с опережением.
А нельзя ли просто послать еще один сигнал синхронизации через секунду после первого? И по нему передвинуть все часы (неподвижные и подвижные) на секунду вперед? Нет, нельзя этого сделать. Потому что сигнал синхронизации в обеих СО должен посылаться из точки начала отсчета. А начало отсчета у них совпадает только однажды, при посылке первого сигнала, через секунду это уже будут две разные точки, и, следовательно, два разных сигнала. Если же послать второй сигнал только из нулевой точки СО, которую мы считаем неподвижной, то он, конечно же, придет к удаляющимся часам движущейся СО с большей задержкой, чем к приближающимся, но это будет всего лишь наш «старый знакомый» – эффект Доплера, а не эффект теории относительности. Кстати, это очень частая ошибка людей, критикующих СТО: они принимают эффект Доплера за «очевидный» факт, противоречащий СТО. Дело в том, что эффект Доплера перекрывает и маскирует релятивистское замедление времени. Для удаляющихся от наблюдателя часов (и при ошибочно выбранном источнике сигналов синхронизации, принадлежащем «чужой» СО), он усиливает замедление времени, добавляя к релятивистскому замедлению времени кажущееся замедление, связанное с доплеровским падением частоты. Для приближающихся часов, он перекрывает по величине релятивистское замедление времени, и создаёт ложное впечатление, что часы идут «ускоренно». Именно поэтому так важно было заранее детально разобраться с эффектом Доплера.
Как же правильно определить, замедлился ли ход движущихся часов? Очень просто! Для того, чтобы зафиксировать скорость хода движущихся часов, надо последовательно зафиксировать их показания в двух точках траектории, сравнив с показаниями синхронизированных часов неподвижной СО, расположенных в тех же точках, т.е., с показаниями двух разных неподвижных часов.
И легко доказать, при помощи умозрительного эксперимента, что, если длины отрезков движущейся СО сокращаются в «К» раз, с чем мы уже согласились, то и ход часов движущейся СО должен замедляться ровно в «К» раз:
Действительно, представим, что движущиеся часы пролетают (со скоростью V) отрезок длиной L неподвижной СО за время T. Теперь взглянем на тот же промежуток времени из СО часов: часы в ней неподвижны, а мимо пролетает, всё с той же скоростью V, укоротившийся отрезок L, имеющий длину L`=KL. Понятно, что время пролёта отрезка сократилось в той же пропорции, и на часах пройдет время T`=KT. Вот, собственно, и все объяснение.
Но, для большей наглядности, сопроводим мысленный эксперимент рисунками, на которых воображаемые часы движутся вдоль линейки длиной L со скоростью V. Я выбрал здесь скорость V=0.86C (0.86 скорости света), при которой коэффициент Лоренца (тут уж мне пришлость посчитать) равен примерно 1/2, следовательно, длины движущихся тел сокращаются в два раза. А длину отрезка выбрал такой, чтобы часы пролетали вдоль линейки ровно за секунду, т.е., L=0.86 световой секунды.
Рисунков, как мы уже, надеюсь, привыкли, требуется два: один сделаем в СО линейки (когда линейка полагается неподвижной), другой – в СО движущихся часов (когда часы полагаются неподвижными, а линейка – движущейся).
На рис.1.а «синяя» линейка длиной L неподвижна, и движущиеся часы («зеленые») пролетают её за время T=1сек. Пара неподвижных часов, закрепленные на концах линейки синхронно показывает Т=0 в начальный момент, и синхронно показывает T=1сек, на момент окончания полёта «зеленых» часов вдоль линейки.
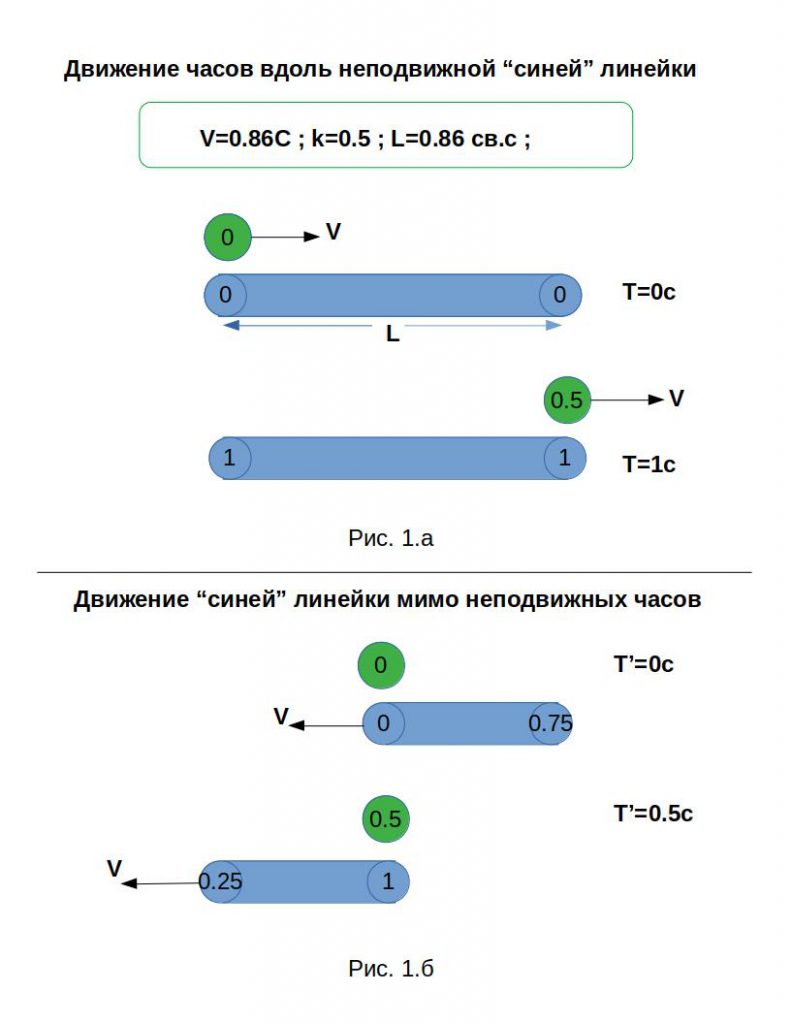
На рис.1.б «зеленые» часы полагаются неподвижными, а мимо них пролетает укороченная «синяя» линейка (длиной L`=0.5L). Совершенно очевидно, что время пролёта укороченной вдвое линейки, займет, по «зеленым» часам, половинное время: T`=0.5T.
Для завершения картины, нам осталось выяснить, какое время на рис.1.б (в СО «зеленых» часов), показывают часы на концах «синей» линейки? Мы точно знаем, что первые из них в начальный момент времени показывали, как и «зеленые», ноль; а вторые часы показали Т=1, когда оказались напротив «зеленых» часов в конце полёта. Но какое время показывали вторые часы, на правом конце линейки, в начале полета, и какое время покажут удалившиеся первые часы на левом конце линейки в конце полета? Мы уже твердо знаем, что удаленные часы движущейся СО, не только могут, но ДОЛЖНЫ показывать другое время, чем часы, находящиеся рядом (мы это поняли еще тогда, когда столкнулись с относительностью одновременности). Теперь нам осталось сообразить, какое время должно быть на правом конце «синей» линейки, чтобы эти «синие» часы шли в 2 раза медленнее зеленых часов, и на момент, когда поравняются с «зелеными», они показывали Т=1. Да проще простого — часы эти на момент T`=0 должны показывать Т=0.75; тогда, на момент T`=0.5, они пройдут четверть секунды и покажут Т=1. Еще проще с первыми часами. Они, на момент T`=0.5, удалятся на расстояние 0.5L влево, и покажут время T=0.25, они ведь тоже идут в два раза медленнее.
Теперь, уже для самостоятельного упражнения и закрепления пройденного, предлагаю Вам еще пару рисунков (рис.2.а и рис.2.б), на которых те же «зеленые» часы и та же «синяя» линейка, но теперь «зеленые» часы расположены на своей («зеленой») линейке всё той же длины L, и добавлены еще одни «зеленые» часы на правом конце этой линейки. Вам предлагается (не заглядывая в ответ в конце главы!) определить, какое время будет на добавленных «зеленых» часах на рис.2.а, на моменты T=0 и T=1, по часам условно неподвижной «синей» линейки:
T’=?; T”=?
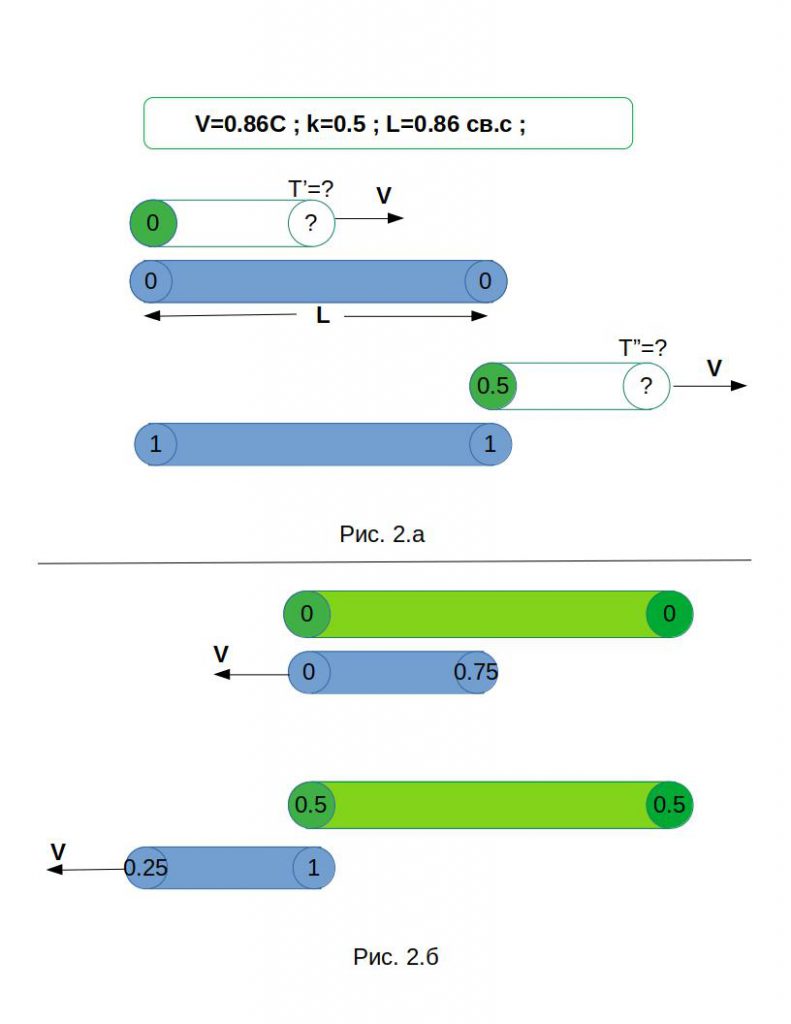
Решили? Сошлось?
Бинго!
Черновой вариант этой главы содержал одну лишь короткую главу из гениального Венички Ерофеева: «И немедленно выпил».©*
Но теперь и мы имеем с Вами полное, законное право выпить. Потому что основное содержание СТО мы освоили.
(ответ к рис.2: T’= -0.75; T”= -0.25 )
____________________________
* В.Ерофеев. «Москва — Петушки», глава «Серп и молот — Карачарово»
Приложение: Ура! Формулы!
Я чувствую, как те из Вас, кто не может жить без формул, кто привык к такому примерно стилю изложения – “…из формул (4) и (5) мы приходим к выражению (6), из которого подстановкой, согласно правилу (1а), получаем выражение (7)… и т.д.” – как все эти люди уже физически изнемогают в ожидании математических формул, подобно рыбам, выброшенным на сушу.
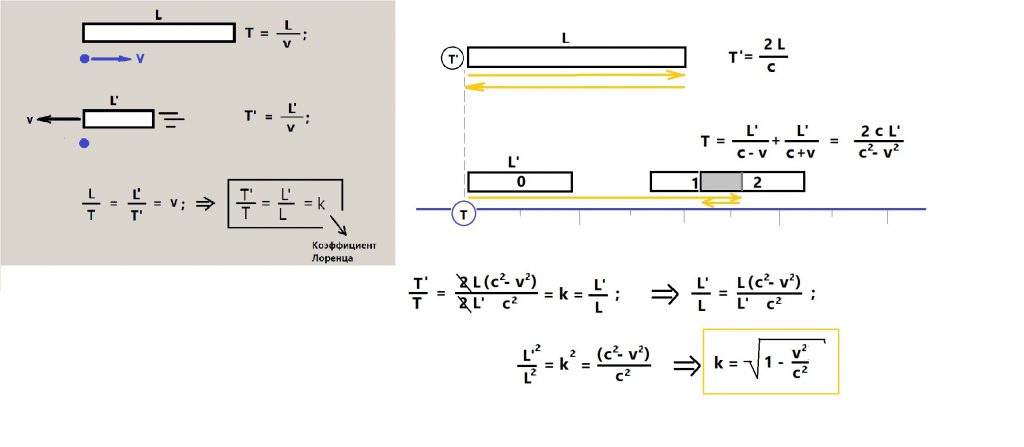
Ну вот и формулы, пожалуйста. Они настолько просты, что доступны каждому школьнику.
На первой картинке (слева) объясняется, что, если длина тела сокращается для движущегося наблюдателя (показан синей точкой), по сравнению с собственной длиной тела в покое, то и течение времени (ход часов этого наблюдателя) замедляется в той же пропорции, относительно времени, отсчитываемого в ИСО покоящегоя тела:
L’/L = T’/T .
Это соотношение и определяет хорощо всем известный коэффициент Лоренца. Простенький, совсем школьный, вывод формулы для него показан справа. Он основан на пробегании луча света туда-обратно вдоль линейки c собственной длиной L, при наблюдении из двух СО: одной, в которой линейка неподвижна, и другой, в которой та же линейка движется со скоростью ‘v’.
Не стану его разбирать подробно. Теперь уже думайте сами, своей головой, дорогой читатель.
Не правда ли, какие простые формулы, в плане математики? И какая огромная сложность – понять их физический смысл.
Приложение 2 – “Четырехмерное пространство и диаграммы Минковского” – читайте на отдельной странице:
Четырехмерное пространство и диаграммы Минковского
Послесловие
Когда я закончил эту статью (или книжку, если угодно), я дал прочесть её моему давнему другу и однокласснику Диме Строганову. Он как раз был одним из тех немногих людей, кто заинтриговал меня Теорией Относительности в юности, и с кем мы изредка беседовали о свойствах света еще в школьные и студенческие годы. Дима – по образованию физик, поработавший в «предперестроечные» годы в знаменитом институте им. Иоффе, и много более меня продвинувшийся в изучении теоретической физики. Мне, разумеется, было интересно его мнение.
В ответ Дима прислал письмо, которое я привожу здесь почти полностью, потому что, во-первых, оно служит приятным для меня свидетельством, что всё написанное выше – не полная ерунда, и представляет какую-то ценность для изучающих СТО. Во-вторых, я полагаю, интересно и полезно прочесть письмо тем, кто собирается идти дальше в изучении физики:
«… надо всегда помнить, что это всё попытки как-то объяснить природу через те понятия и представления, которые доступны нам с точки зрения наших органов чувств. К чему мы привыкли из собственного чувственного опыта. И это совершенно правильно на определённом этапе достижения понимания.
На следующем же этапе (можно назвать его более «профессиональным») неизбежно абстрагирование от этих понятий и представлений, и переход на язык математики, который помогает нам понять и сформулировать, в частности, то, что мы не можем себе наглядно представить (как, например, непредставим для человека с нормальной психикой 4-х или 5-и мерный куб) – так как в нашей реальной жизни ничего подобного мы ни увидеть, ни ощутить/потрогать (и т.п.) не можем.
И получается так – толчками для истинно прорывных, революционных изменений наших представлений о природе служат такие мысленные эксперименты, которые потом формализуются в виде адекватных математических аппаратов. Из которых потом получаются такие выводы, которые могут быть уже недоступны для понимания на уровне «квази-/полу- классических» мысленных экспериментов. Самая первая иллюстрация этого, которая мне приходит в голову, это «черные дыры» и связанные с этим понятия – горизонт событий, сфера Шварцшильда и т.п. (в частности, потому, что на горизонте событий свет, можно сказать, «останавливается» – и получается невозможная «остановившаяся» электромагнитная волна).
Поэтому в классическом курсе теорфизики Ландау-Лившица СТО просто начинается с определённых постулатов, сразу же облечённых в вид формул (их считанное число и, конечно, эти постулаты – результаты экспериментов, как реальных, так и «мысленных»). А конкретно, с утверждения, что движение материальной точки, подчиняющееся, как и в классической механике, принципу наименьшего действия, описывается так называемой функцией Лагранжа, которая просто имеет другой вид, чем у Ньютона. И которая превращается в «ньютоновский» лагранжиан, если скорость точки много меньше “с”. Т.е. постулируется не то, что непосредственно доступно нашим органам чувств (или даже пусть и недоступно, но «понятно» по аналогии с тем, что доступно), а некоторые совершенно абстрактные понятия.
А то, что ты написал, очень важно и нужно (для профессионала) на этапе «слома» психологических границ, чтобы это профессионал не боялся приходить к таким выводам, которые с точки зрения «здравого смысла» невозможны – потому, что «такого не может быть никогда»; потому, что этому невозможно найти никаких аналогов в «нашем мире». Ну, и, конечно, как пример того, как поиски новых сущностей «наощупь» (т.е. всё время отталкиваясь от известного и представимого) открывают путь к формализуемым обобщениям.»
